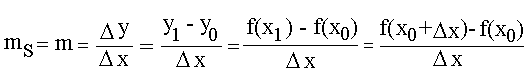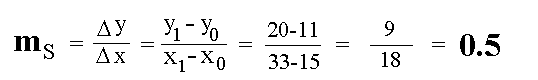Sekantensteigung

      Da eine Sekante formal nichts anderes als eine Gerade ist,
      berechnet sich die "Steigung m_s der Sekante" nach den gleichen
      Formeln, mit der man die "Steigung m einer Geraden" berechnet.
      Diese Formeln haben wir bereits auf der vorletzten Seite hergeleitet:

     

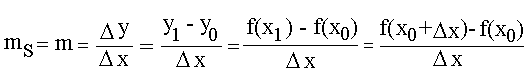
      Bei Bedarf kann man sich die Formeln am nachfolgenden
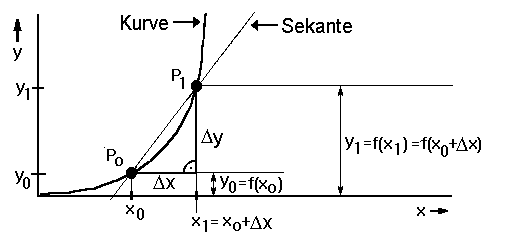
      (uns bereits bekannten) Bild nochmals verdeutlichen:

Der Differenzenquotient
      Die Sekantensteigung m_s nennt auch den Differenzenquotienten.
      Der Name Differenzenquotient kommt daher, dass im Zähler
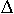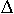      (y=y₁-y₀) und im Nenner (x=x₁-x₀) Differenzen stehen.

      Achtung: Den Differenzenquotienten darf man nicht mit den
      Differentialquotienten verwechseln, den wir später  
      kennenlernen werden.

Bedeutung der Sekantensteigung
      Die Sekantensteigung m_s gibt den durchschnittliche Steigung
      der Kurve zwischen den Punkten P₀ und P₁ an. Beispiel:

      Die Sekante (Bild oben) gehe durch die Punkte P₀=(15/11)
      und Punkt P₁=(33/20). Wie groß ist die durchschnittliche
      Steigung m_s der Kurve zwischen den Punkten P₀ und P₁?
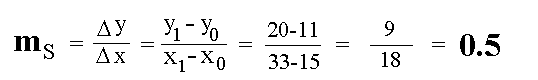