Version: Test |
Differentialrechnung II ZURÜCK |
| Info-Seite | Vorkenntnisse: .... Was wird gelernt: .... Infos:www.mathematik.net |
| Tangentensteigung der Funktion y=x² |
Als Anwendungsbeispiel der "Formel der
Tangentensteigung" leiten wir die Steigung der Funktion f(x) = x² her. Sie lautet: f '(x) = 2x |
| Beispiel | Berechnung der Tangentensteigung der Funktion y=x² im Punkt x0 |
| Ableitung | Da der Grenzwert lim ... nicht immer nur eine geometrische
Bedeutung (Tangentensteigung) hat, benutzt man die allgemeineren Begriffe Ableitung bzw. Differentialquotient. |
| Ableitungsfunktion | Bildet man zu jeder Stelle einer Funktion die Ableitung,
so ensteht eine neue Funktion, genannt: Ableitungsfunktion (meist aber nur Ableitung). |
| Ableitung einer konstanten Funktion |
f(x) = C  f '(x) = 0 |
| Ableitung der Potenzfunktion |
f(x) = xn
f '(x) = n·xn-1 |
| Ableitung der Wurzelfunktion | Das man jede Wurzel als Potenz mit rationalen Exponenten
schreiben kann, kann man mit der Potenzregel auch Wurzelfunktionen ableiten. |
| Ableitungen trigonometrischer Funktionen |
f(x) = sin x f '(x) = cos x f(x) = cos x f '(x) = -sin x f(x) = tan x f '(x) = 1/(cos²x)f(x) = cot x f '(x) = -(1/sin²x) |
| Ableitung der allgemeinen Exponential- funktion |
 |
| Ableitung der natürlichen Exponential- funktion |
 |
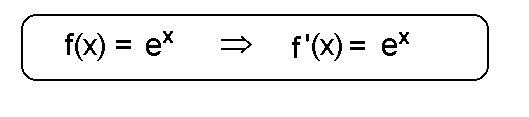| Ableitung der allgemeinen Logarithmus- funktion |
 |
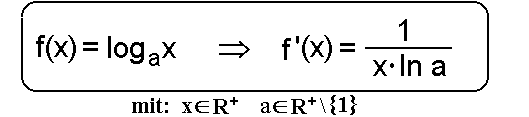| Ableitung der natürlichen Logarithmus- funktion |
 |
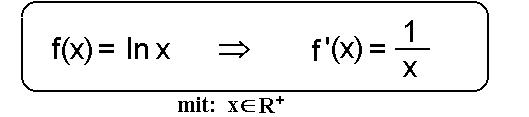