Beispiel:
Tangentensteigung
der Funktion y=x²
|
 Vorbemerkung
Im Kapitel I haben wir eine Formel für die Tangentensteigung mt
im Punkt x0 hergeleitet. Aus dieser allgemeinen Formel (gilt für
alle Funktionen) kann man Formeln für die Tangentensteigung mt
von konkreten Funktionen herleiten, z.B. für die Funktion y=x²: Vorbemerkung
Im Kapitel I haben wir eine Formel für die Tangentensteigung mt
im Punkt x0 hergeleitet. Aus dieser allgemeinen Formel (gilt für
alle Funktionen) kann man Formeln für die Tangentensteigung mt
von konkreten Funktionen herleiten, z.B. für die Funktion y=x²:
 Die Herleitung
Am Ende des vorigen Kapitels hatten wir eine Formel für die
Tangentensteigung mt im Punkt x0 hergeleitet: Die Herleitung
Am Ende des vorigen Kapitels hatten wir eine Formel für die
Tangentensteigung mt im Punkt x0 hergeleitet:
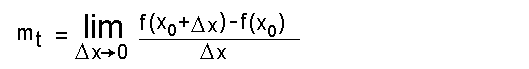 Wie gesagt, wollen wir nun daraus die Steigung der Funktion y=x²
bestimmen. Der Funktionswert f an der Stelle (x0) ist dann (x0)²,
der Funktionswert f an der Stelle (x0+
Wie gesagt, wollen wir nun daraus die Steigung der Funktion y=x²
bestimmen. Der Funktionswert f an der Stelle (x0) ist dann (x0)²,
der Funktionswert f an der Stelle (x0+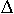 x) ist (x0+ x) ist (x0+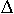 x)²: x)²:
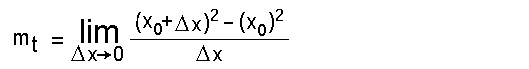 Nun vereinfachen wir den Zähler des Bruches.
Den Term (x0+
Nun vereinfachen wir den Zähler des Bruches.
Den Term (x0+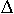 x)² kann man ausmultiplizieren: x)² kann man ausmultiplizieren:
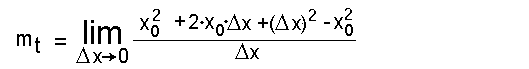 Der erste und der letzte Summand heben sich auf:
Der erste und der letzte Summand heben sich auf:
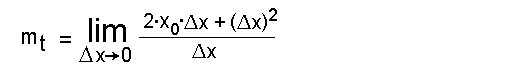 Im Zähler klammern wir
Im Zähler klammern wir 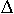 x aus, und kürzen mit dem Nenner: x aus, und kürzen mit dem Nenner:
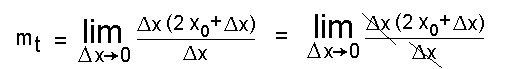 Nun bilden wir den Grenzwert (limes) für
Nun bilden wir den Grenzwert (limes) für 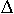 x gegen 0: x gegen 0:
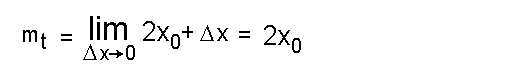 Die Funktion (Kurve) y=x² hat an der Stelle x0 die Steigung mt = 2x0:
Die Funktion (Kurve) y=x² hat an der Stelle x0 die Steigung mt = 2x0:
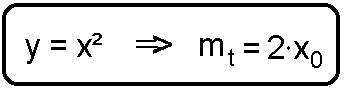
|