Beispiel zur
Formel
|
 Worum geht's
Auf der Vorseite haben wir eine Formel hergeleitet, mit der man
die Steigung der Funktion y=x² in einem beliebigen Punkt x0
bestimmen kann: Worum geht's
Auf der Vorseite haben wir eine Formel hergeleitet, mit der man
die Steigung der Funktion y=x² in einem beliebigen Punkt x0
bestimmen kann:
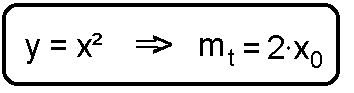 Nun wollen wir ein Beispiel mit dieser Formel berechnen.
Nun wollen wir ein Beispiel mit dieser Formel berechnen.
 Das Beispiel
Wie gesagt sei die Funktion y=x² gegeben. Gesucht sei
die Steigung im Punkt P = (1.5/f(1.5)) = (1.5/2.25).
Wir nehmen die Formel und setzen ein:
mt = 2·x0 = 2·1.5 = 3
Die Steigung der Funktion y=x² im Punkt (1.5/2.25) hat den Wert 3. Das Beispiel
Wie gesagt sei die Funktion y=x² gegeben. Gesucht sei
die Steigung im Punkt P = (1.5/f(1.5)) = (1.5/2.25).
Wir nehmen die Formel und setzen ein:
mt = 2·x0 = 2·1.5 = 3
Die Steigung der Funktion y=x² im Punkt (1.5/2.25) hat den Wert 3.
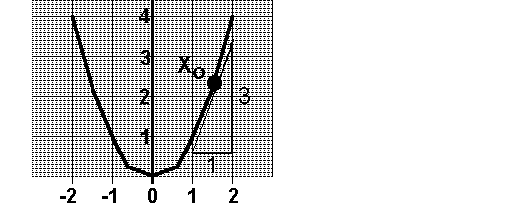
 Das Bild zum Beispiel
Im Bild ist der Punkt x0=(1.5/2.25) eingezeichnet und die
Tangente an diesen Punkt, die die Steigung 3 hat: Das Bild zum Beispiel
Im Bild ist der Punkt x0=(1.5/2.25) eingezeichnet und die
Tangente an diesen Punkt, die die Steigung 3 hat:
|