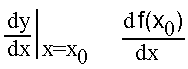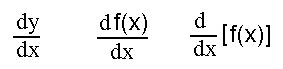Auf der Vorseite haben wir den Begriff Ableitung im Punkt x₀
      eingeführt. Auf dieser Seite erklären wir den Unterschied
      zwischen Ableitung im Punkt x₀ und Ableitung.

      Wir zeichen eine beliebige Funktion (hier: y=x²) in ein
      Koordinatensytem ein. Nun bilden wir die Ableitung
      des Punktes P₀(1.5/f(1.5)), und tragen sie in ein zweites
      darunterliegendes Koordinatensystem ein: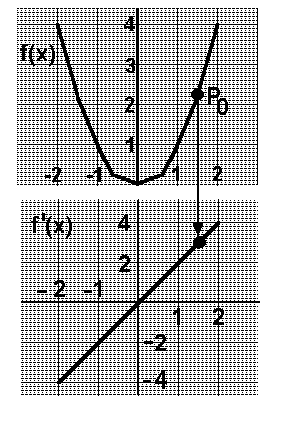

     
      Würde man nun zu jedem Punkt x₀/y₀ der Funktion f(x) die
       Ableitung f '(x₀) bestimmen, und in das darunterliegende
       Koordinatensystem eintragen, so entstände eine neue
       Funktion, die man die Ableitung f '(x) nennt.

Ableitung im Punkt x0	Ableitungsfunktion
f '(x0)	f '(x)
y '(x0)	y'

      Der Ausdruck nennt sich Differentialoperator.
      Wendet man ihn auf eine Funktion f(x) an, so erzeugt er
      die dazugehörige Ableitung f '(x).