Ableitung der
Potenzfunktion
(Potenzregel)
|
 Worum geht's
Bis jetzt haben wir nur die Ableitung der Funktion y=x2 kennen-
gelernt. Jetzt geht's um die Ableitung der Funktion y=xn mit n Worum geht's
Bis jetzt haben wir nur die Ableitung der Funktion y=x2 kennen-
gelernt. Jetzt geht's um die Ableitung der Funktion y=xn mit n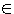 Q. Q.
 Die Potenzregel
Ist die Funktion f(x) = xn mit n Die Potenzregel
Ist die Funktion f(x) = xn mit n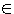 Q gegeben, so lautet die
dazugehörige Ableitung f '(x) = n·xn-1 Q gegeben, so lautet die
dazugehörige Ableitung f '(x) = n·xn-1
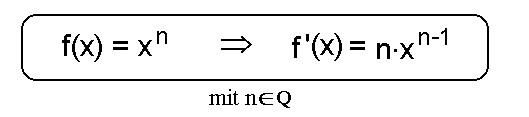
 Beispiel
Auf dieser Seite zuerst ein Beispiel, bei dem n Beispiel
Auf dieser Seite zuerst ein Beispiel, bei dem n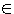 N
Gegeben: Die Funktion f(x) = x7
Gesucht: 1. Die Ableitung f '(x)
2. Die Ableitung an der Stelle x0=1
Lösung: Zur Lösung benutzt man die Potenzregel:
f '(x) = n·xn-1 = 7·x7-1 = 7·x6
Nun bestimmen wir die Ableitung an der Stelle x0=1:
f '(x0) = 7·(x0)6 = 7·16 = 7 N
Gegeben: Die Funktion f(x) = x7
Gesucht: 1. Die Ableitung f '(x)
2. Die Ableitung an der Stelle x0=1
Lösung: Zur Lösung benutzt man die Potenzregel:
f '(x) = n·xn-1 = 7·x7-1 = 7·x6
Nun bestimmen wir die Ableitung an der Stelle x0=1:
f '(x0) = 7·(x0)6 = 7·16 = 7
|