Ableitung der Wurzelfunktion
Nungeht es um die Ableitung von Wurzelfunktionen.
Am nachfolgenden Beispiel sehen wir, daß wir dazu keine
"Wurzelregel" brauchen, sondern daß wir mit der Potenzregel
(siehe vorige Seite) auch jede Wurzelfunktionen ableiten können.
Beispiel
Der Trick besteht darin, daß wir die Wurzel einfach als Potenz
mit rationalen Exponenten schreiben:
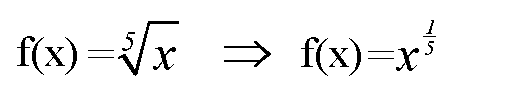Da die Funktion nun nicht mehr als Wurzelfunktion sondern als
Potenzfunktion vorliegt, können wir die Funktion mit Hilfe
der Potenzregel ableiten:
Ableitung der Wurzelfunktion
Nun geht es um die Ableitung von Wurzelfunktionen.
Am nachfolgenden Beispiel sehen wir, daß wir dazu keine
"Wurzelregel" brauchen, sondern daß wir mit der Potenzregel
(siehe vorige Seite) auch jede Wurzelfunktionen ableiten können.
Da die Funktion nun nicht mehr als Wurzelfunktion sondern als
Potenzfunktion vorliegt, können wir die Funktion mit Hilfe
der Potenzregel ableiten:
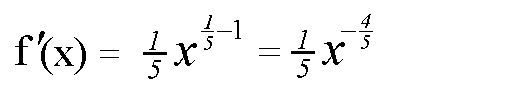
