Ableitung der
natürlichen
Exponential-
funktion
|
 Die natürliche Exponentialfunktion
Ein Spezialfall der allgemeinen Exponentialfunktion y=ax (a Die natürliche Exponentialfunktion
Ein Spezialfall der allgemeinen Exponentialfunktion y=ax (a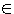 R+)
ist die natürliche Exponentialfunktion y=ex (e=2.718...).
Ihre Ableitung wollen wir auf dieser Seite kennenlernen. R+)
ist die natürliche Exponentialfunktion y=ex (e=2.718...).
Ihre Ableitung wollen wir auf dieser Seite kennenlernen.
 Ableitung der natürlichen Exponentialfunktion
Mit der Ableitung der natürlichen Exponentialfunktion hat es eine
besondere Bewandnis. Die natürliche Exponentialfunktion ist die
einzige Funktion, bei der die ursprüngliche Funktion und die von
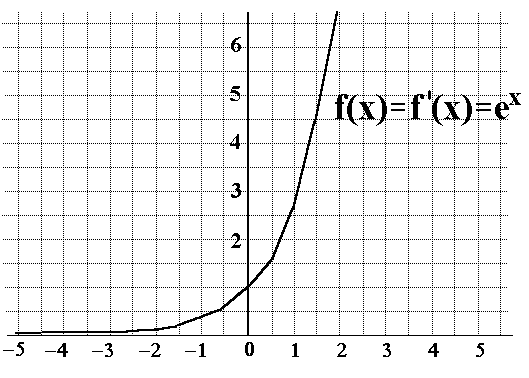
ihr abgeleitete Funktion identisch sind. Als Formel: f(x) = f '(x). Ableitung der natürlichen Exponentialfunktion
Mit der Ableitung der natürlichen Exponentialfunktion hat es eine
besondere Bewandnis. Die natürliche Exponentialfunktion ist die
einzige Funktion, bei der die ursprüngliche Funktion und die von
ihr abgeleitete Funktion identisch sind. Als Formel: f(x) = f '(x).
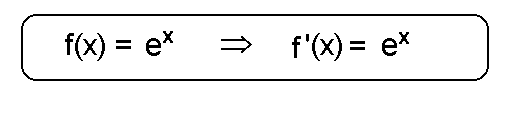
 Bild Bild
|