Ableitung der
natürlichen
Logarithmus-
funktion
|
 Die natürliche Logarithmusfunktion
Ein Spezialfall der Logarithmusfunktion y=logax x Die natürliche Logarithmusfunktion
Ein Spezialfall der Logarithmusfunktion y=logax x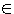 R+ a R+ a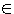 R+\{1}
ist die natürliche Logarithmusfunktion y=ln x mit: x R+\{1}
ist die natürliche Logarithmusfunktion y=ln x mit: x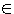 R+
Auf dieser Seite wollen wir ihre Ableitung kennenlernen. R+
Auf dieser Seite wollen wir ihre Ableitung kennenlernen.
 Ableitung der natürlich.Logarithmusfunktion Ableitung der natürlich.Logarithmusfunktion
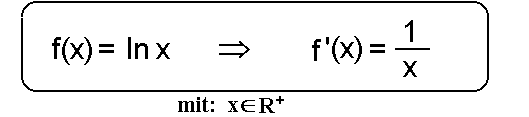
 Beispiel
Gegeben: Die Funktion f(x) = ln (x)
Gesucht: 1. Die Ableitung f '(x)
2. Die Ableitung an der Stelle x0=10
Lösung: Zur Lösung benutzt man die eingerahmte Formel:
f '(x) = 1/x
Nun bestimmen wir die Ableitung an der Stelle x0=10:
f '(x0)= 1/x0 = 1/10 = 0.1 Beispiel
Gegeben: Die Funktion f(x) = ln (x)
Gesucht: 1. Die Ableitung f '(x)
2. Die Ableitung an der Stelle x0=10
Lösung: Zur Lösung benutzt man die eingerahmte Formel:
f '(x) = 1/x
Nun bestimmen wir die Ableitung an der Stelle x0=10:
f '(x0)= 1/x0 = 1/10 = 0.1
|