Auf der vorigen Seite haben wir schon gesagt, daß die Basis a
der Exponentialfunkton f(x)=a^x immer positiv sein muß.
Nun müssen wir für positive a nochmals zwei Fälle unterscheiden,
und zwar den Fall 0<a<1 und den Fall a>1.

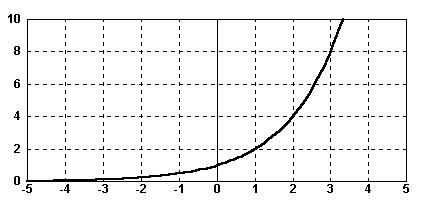
Wenn a>1 ist, dann ist die Exponentialfunktion streng monoton steigend,
d.h. die Funktionswerte nehmen von links nach rechtsbeständig zu.

Die Funktionswerte nehmen von links nach rechts nicht nur ständig zu,
die Funktionswerte gehen sogar gegen Unendlich.
Beachte: Nicht jede streng monoton steigende Funktion geht auch automatisch
gegen Unendlich, sie könnte auch konvergieren, mehr im Kurs Grenzwerte).

Je mehr man auf der x-Achse nach links geht (ins Unendliche),
desto mehr schmiegt sich der Graph an die x-Achse an.