Nun betrachten wir Exponentialfunktionen mit verschiedener Basis,
wobei die Basis größer 1 sein soll:

          f(x)=a^x       mit: a>1

Im Beispiel vergleichen wir die Funktionen f(x)=2^x und f(x)=3^x:

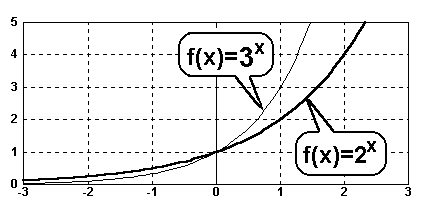
Für positive x gilt:
Die Exponentialfunktion mit der Basis 3 verläuft oberhalb der
Exponentialfunktion mit der Basis 2. Eine große Basis erzeugt also
einen steiler anwachsenden Graphen, d.h. die Exponentialfunktion
mit großer Basis verläuft oberhalb der Exponentialfunktion mit kleiner Basis.

Für negative x gilt:
Die Exponentialfunktion mit der Basis 3 verläuft nun unterhalb der
Exponentialfunktion mit der Basis 2. Eine Exponentialfunktion
mit großer Basis nähert sich also schneller der x-Achse, als eine
Exponentialfunktion mit kleiner Basis.

Merkregel (für a>1):
Ist die Basis groß, geht die Exponentialfunktion schnell ins Unendliche,
und nähert sich schnell der x-Achse.