Nun betrachten wir Exponentialfunktionen mit verschiedener Basis,
wobei für die Basis a gelten soll: 0<a<1

          f(x)=a^x       mit: 0<a<1

Im Beispiel vergleichen wir die Funktionen f(x)=0.5^x und f(x)=0.2^x:

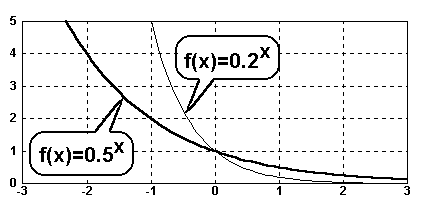
Für positive x gilt:
Die Exponentialfunktion mit der Basis 0.2 verläuft nun unterhalb der
Exponentialfunktion mit der Basis 0.5. Eine Exponentialfunktion
mit kleiner Basis nähert sich also schneller der x-Achse, als eine
Exponentialfunktion mit größerer Basis (0<a<1).

Für negative x gilt:
Die Exponentialfunktion mit der Basis 0.2 verläuft oberhalb der
Exponentialfunktion mit der Basis 0.5. Eine kleine Basis (0<a<1)
erzeugt also einen steiler anwachsenden Graphen, d.h. die Exponentialfunktion
mit kleiner Basis verläuft oberhalb der Exponentialfunktion mit größerer Basis.

Merkregel für 0<a<1:
Ist die Basis a klein, geht die Exponentialfunktion schnell ins Unendliche,
und nähert sich schnell der x-Achse.