Auf der vorigen Seite haben wir gesagt:

Wenn man bei der Funktion f(x)=a^x von der Basis a den Kehrwert bildet,
entsteht eine Funktion g(x)=(1/a)^x . Die Graphen der beiden Funktionen
liegen spiegelbild bezüglich der y-Achse zueinander.

    
   f(x) = a^x   liegt spiegelbildlich bzgl. y-Achse zu    g(x) = (1/a)^x
    
Nun werden wir zeigen, daß es noch eine andere Möglichkeit gibt,
diese spiegelbildlich zur y-Achse liegende Funktion zu finden. Es gilt:

Wenn man bei der Funktion f(x)=a^x das Vorzeichen des Exponenten negiert,
entsteht eine Funktion g'(x)=a^–x . Die Graphen der beiden Funktionen
liegen wieder spiegelbild bezüglich der y-Achse zueinander.

   f(x) = a^x   liegt spiegelbildlich bzgl. y-Achse zu     g'(x) = a^–x
   

Wir beweisen, daß die Funktion g(x)=(1/a)^x und g'(x)=a^–x gleich sind:

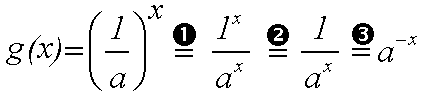
Erklärung der Umformungen:
  Hier wurden ein Potenzgesetz angewendet.
Wenn man die Zahl 1 mit irgendeiner Zahl x potenziert,
      dann kommt auf jeden Fall wieder die Zahl 1 heraus.
  Hier wurden ein Potenzgesetz angewendet.