Stauchung
in Richtung
der x-Achse:
y=an·x (n>1) |
 |
Satz |
|
Gegeben sei die Exponentialfunktion:
f(x)=ax
Beispiel: f(x)=2x
Wird der Exponent nun mit einer Zahl n>1 multipliziert:
g(x)=an·x Beispiel: g(x)=24x
so entsteht ein Graph, der gegenüber der ursprünglichen Funktion
auf das 1/n-fache in die x-Richtung gestaucht ist. |
|
 |
Bild und Erklärung |
|
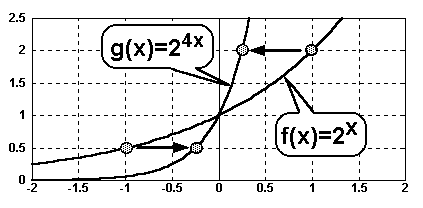
Als Beispiel betrachten wir die
Funktionen im Bild oben:
f(x)= 2x
und die gestauchte Funktion: g(x)= 24x
Die Funktion g(x) erreicht einen bestimmten Funktionswert (z.B. y=2)
zu einen fünfmal früheren Zeitpunkt als die Funktion f(x). Die Funktion
g(x) erscheint um den Faktor 5 in Richtung der positiven x-Achse gestaucht
Geht man auf der x-Achse in negativer Richtung, so ereicht g(x) einen
bestimmten Funktionswert (z.B. 0.5) ebenfalls fünfmal früher.
Die Funktion g(x) erscheint in Richtung der negativen x-Achse gestaucht. |
|