Version: Test ©Raddy 2000	Inhalt zu: Gruppen IV ZURÜCK
Info-Seite	Vorkenntnisse: ... Themen: ... Infos: www.mathematik.net
Untergruppen	Gegeben sei eine Gruppe G und ein Gebilde G'. Das Gebilde G' nennt man dann *Untergruppe G'* der Gruppe G, wenn das Gebilde G' folgende drei Bedingungen erfüllt: G' liegt die gleiche Verknüpfung R zugrunde wie der Gruppe G G' liegt eine nichtleere Teilmenge G' der Menge G zugrunde Das Gebilde G' ist selbst wieder eine Gruppe
Beispiel 1:	Im Kapitel I haben wir die Gruppe G der 2x2-Matrizen kennengelernt. (Menge der 2x2-Matrizen zusammen mit der Matrix-Addition). Eine Untergruppe G' dieser Gruppe besteht aus der Menge der "2x2-Diagonalmatrizen" zusammen mit der Matrix-Addition: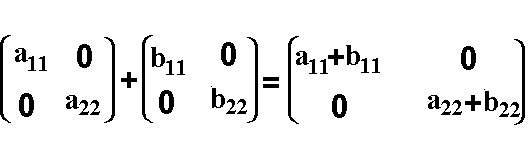
Untergruppen- kriterium	Muß man überprüfen, ob das Gebilde G' eine Untergruppe von G ist, so muß man nur die folgenden vier Bedingungen überprüfen: Die Verknüpfung R im Gebilde G' muß die gleiche wie in G sein Die Menge G' muß eine nichtleere Teilmenge von G sein Die Verknüpfung R muß auch in der Teilmenge G'G abgeschlossen sein Existiert zu jedem Element g' der Teilmenge G' ein inverses Element, und liegt dies in der Teilmenge G'
Beispiel 2:	Gegeben sei die Gruppe der Drehungen eines Quadrates die wir im Kapitel Gruppen II kennengelernt haben. Dann ist die Gruppe der Drehungen um z·90° zZ eine Untergruppe dieser Gruppe.
Beispiel 3:	Gegeben sei die Gruppe der Euklidische Vektoren der Ebene, die wir im Kapitel Gruppen III kennengelernt haben. Dann ist die Gruppe der Euklidische Vektoren einer Geraden der Ebene eine Untergruppe dieser Gruppe.