Version: Test |
Gruppen IV ZURÜCK |
| Beispiel |  BeispielIm Kapitel I haben wir die Gruppe G der 2x2-Matrizen kennengelernt. (Menge der 2x2-Matrizen zusammen mit der Matrix-Addition). Eine Untergruppe G' dieser Gruppe besteht aus der Menge der "2x2-Diagonalmatrizen" zusammen mit der Matrix-Addition: 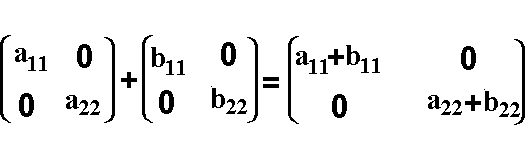 Das es sich hier wirklich um eine Untergruppe handelt, wollen wir nun anhand der Definition einer Untergruppe überprüfen:  Die Verknüpfung ist in G und G' gleich: Die
Matrix-Addition  Die Menge der
"2x2-Diagonalmatrizen" ist einenichtleere Teilmenge der 2x2-Matrizen.  Nun müssen wir überprüfen, ob G'
selbst wieder eineGruppe ist, d.h. H muß alle Gruppenaxiome erfüllen: Abgeschlossenheit: Addiert man zwei "2x2-Diagonalmatrizen", so ist das Ergebnis ebenfalls eine "2x2-Diagonalmatrix". Das Axiom der Abgeschlossenheit ist somit erfüllt. Assoziativgesetz: Wenn das deutsche Strafgesetz in Deutschland gültig ist, dann ist es auch in einer Teilmenge von Deutschland (z.B. in Bayern) gültig. Genauso ist es mit dem Assoziativgesetz: Wenn das Assoziativgesetz in der Menge der 2x2 Matrizen gültig ist, dann ist es auch in der Teilmenge der "2x2-Diagonalmatrizen" gültig. Neutrales Element: Nun müssen wir überprüfen: Gibt es in der Menge der "2x2-Diagonalmatrizen" ein neutrales Element. Ja, es ist eine 2x2-Nullmatrix, die ein Spezialfall einer 2x2-Diagonalmatrix ist. Inverse Elemente: Nun müssen wir überprüfen, ob das inverse Element einer "2x2 Diagonalmatrix" ebenfalls eine "2x2 Diagonalmatrix" ist. Wie man sieht ist dieses Axiom erfüllt: 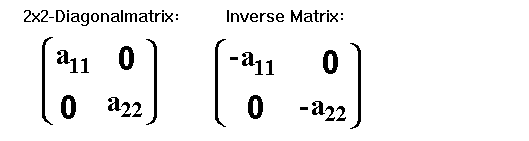 |