Version: Test |
Gruppen IV ZURÜCK |
| Weiteres Beispiel einer Untergruppe: Euklidische Vektoren, die auf einer Geraden der Ebene liegen |
 BeweisGegeben ist die Gruppe G der Euklidischen Vektoren der Ebene die wir aus dem Kapitel Gruppen III kennen. Diese Gruppe besteht aus der Menge der Euklidischen Vektoren der Ebene zusammen mit der Verknüpfung "Vektoraddition". Eine Untergruppe G' dieser Gruppe ist die Menge der Euklischen Vektoren einer Geraden der Ebene, zusammen mit der Verknüpfung "Vektoraddition" aus der Gruppe G. Zum Beweis wird wieder das Untergruppen-Kriterium verwendet. 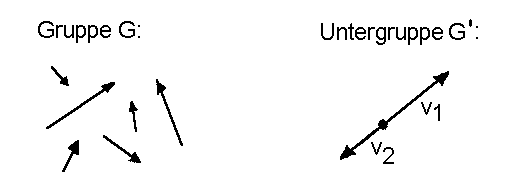 Beweis Wir haben bestimmt,
das die Verknüpfung "Vektoraddition"aus der Gruppe G auch dem Gebilde G' zugrundeliegen soll. Damit ist Bedingung 1 des Untergruppen-Kriteriums erfüllt.  Bedingung 2 des Untergruppen-Kriteriums ist ebenfalls erfüllt,da die Menge der Euklischen Vektoren einer Geraden der Ebene eine nichtleere Teilmenge der Euklidischen Vektoren der Ebene ist.  Die Verknüpfung "Vektoraddition" ist auf der Menge derEuklischen Vektoren einer Geraden der Ebene abgeschlossen. Addiert man nämlich zwei Vektoren, die auf einer Geraden der Ebene liegen, so erhält man einen Vektor, der auf dieser Geraden liegt. Somit ist Bedingung 3 ebenfalls erfüllt.  Zu jedem Euklischen Vektor einer Geraden der Ebene gibt es einen inversen Vektor, der auf dieser Geraden liegt. 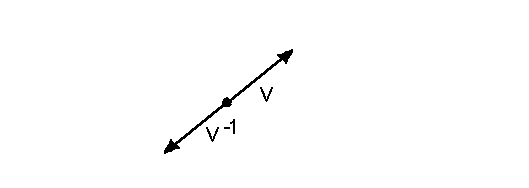 |