Beweis:
Multiplikation mit k |
 |
Beweis |
|
Zunächst beweisen wir den Hilfssatz: Wenn man
im linken Faktor A
des Matrixproduktes A·B eine Zeile n mit k multipliziert, dann entspricht
das einer Multiplikation mit k der gleichen
Zeile n in der Ergebnismatrix (A·B):
An,k · B = (A·B)n,k
Zum Beweis betrachen wir das Bild einer Matrix-Multiplikation der
Matrix A (mit den Zeilenvektoren A1-A3) mit der Matrix B
(mit den Spaltenvektoren B1T, B2T, B3T). Die Definition
der Matrizen-
multiplikation schreibt uns vor, daß man z.B. die erste Zeile von
A1 mit
den Spalten von B skalar multipliziert werden muß, um die Elemente
der ersten Zeile in der Ergebnismatrix zu erhalten:
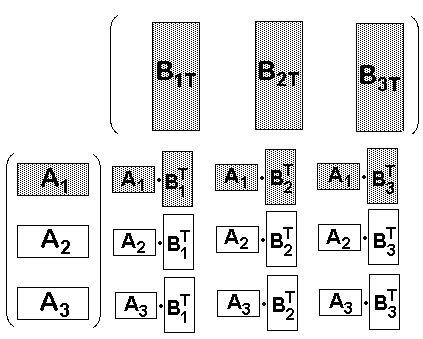
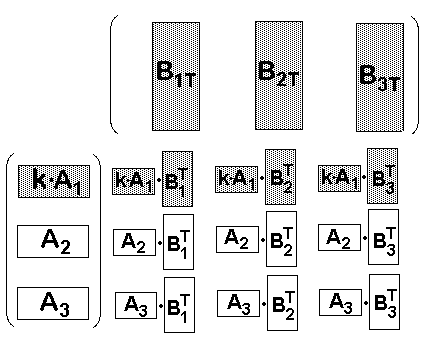
Wenn wir nun z.B. die Zeile A1 mit k multiplizieren, dann wird dadurch
die gleiche Zeile in der Ergebnismatrix (A·B) mit k
multipliziert:
Nun haben wir den Hilfssatz bewiesen:
An,k
· B = (A·B)n,k
Sei nun A eine Einheitsmatrix E dann wird aus (A·B)n,k = (E·B)n,k
= Bn,k
denn die Einheitsmatrix ist das neutrale Element der Matrixmultiplikation:
En,k
· B = Bn,k
Damit ist der Satz bewiesen. |
|