Beweis:
Addition des Vielfachen einer Zeile zu einer anderen Zeile |
 |
Beweis |
|
Zunächst beweisen wir den Hilfssatz: Wenn man
im linken Faktor A des
Matrixproduktes (A·B) zu einer Zeile n das k-fache der Zeile m hinzufügt,
dann entspricht das der Addition des k-fachen Zeile m zur Zeile n in
der Ergebnismatrix (A·B):
An,k,m · B = (A·B)n,k,m
(Gl.1)
Zum Beweis betrachen wir zunächst die linke Seite der Gleichung, und
führen die angegebenen Operationen durch. Als Beispiel addieren wir zur
ersten Zeile A1 das k-fache der dritten Zeile, und führen dann die
Matrix-Multiplikation mit B durch:
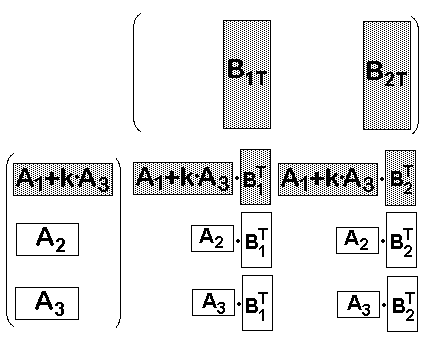
Die Einträge der ersten Zeile in der Ergebnismatrix lauten:
(A1+k·A3)·B1T
(A1+k·A3)·B2T (Gl. 2)
Nun betrachten wir die rechte Seite der Gleichung (1) und führen die
angegebenen Operationen mit den gleichen Zeilen n,m durch:
Wir addieren zur ersten Zeile A1 das k-fache der dritten Zeile A1:
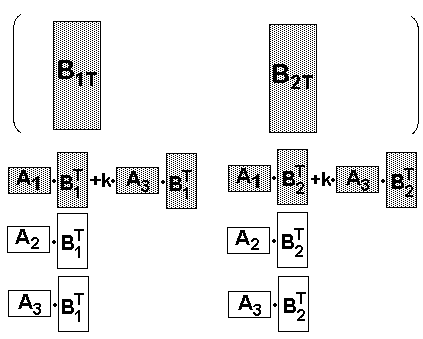
Die Einträge der ersten Zeile in der Ergebnismatrix lauten:
A1·B1T
+ k·A3·B1T
A1·B2T + k·A3·B2T
Wenn wir nun B1T bzw. B2T ausklammern,
sehen wir die
Übereinstimmung mit Gleichung 2. Damit haben wir den Hilfssatz bewiesen:
An,k,m · B
= (A·B)n,k,m
(Gl.1)
Sei nun A eine Einheitsmatrix E dann wird aus (A·B)n,k,m = (E·B)n,k,m
= Bn,k,m
denn die Einheitsmatrix ist das neutrale Element der Matrixmultiplikation:
En,k,m
· B = Bn,k,m
Damit ist der Satz bewiesen. |
|