Lösungsweg für den Fall:
Ungleichung ist in Linearfaktoren zerlegt |
 |
Hinweis zum Trickfilm |
|
Zu dieser Seite gibt es einen Trickfilm mit einem ähnlichen Beispiel.
Du kannst den Film in einem
neuen
Fenster laden, während du diese
Seite liest. Klicke dazu auf folgenden
Link:
Trickfilm:
Der einfachste Fall: Die Ungleichung ist in Linearfaktoren zerlegt
|
 |
Gegeben |
|
Der einfachste Fall einer Polynomungleichung liegt vor, wenn die
Polynomungleichung
in Linearfaktoren zerlegt ist, also Faktoren der Form (x–a) mit
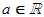 . .
|
 |
Deuten der Ungleichung als
Funktion |
|
Gegeben sei die Polynomungleichung:
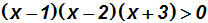
Die linke Seite kann man als Funktion auffassen. Die Frage lautet dann:
Wann ist die Funktion f(x)=(x–1)(x–2)(x+3)
größer als Null:
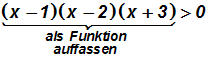
Um nun zu ermitteln, wann die Funktion f(x) größer Null ist, müssen wir
uns ihren
Funktionsverlauf verdeutlichen. Dazu müssen wir zuerst die Nullstellen
bestimmen
und
uns zweitens überlegen, wie die Funktion f(x) für große |x| verläuft.
|
 |
Einzeichnen der Nullstellen |
|
Die Nullstellen der Funktion
f(x)=(x–1)(x–2)(x+3) kann man direkt
vom Funktionsterm ablesen. Die Funktion ist gleich Null, wenn einer der
Faktoren gleich Null ist, also wenn x=1, x=2 oder x=–3.
Wir zeichnen die Nullstellen in ein Koordinantensystem ein:
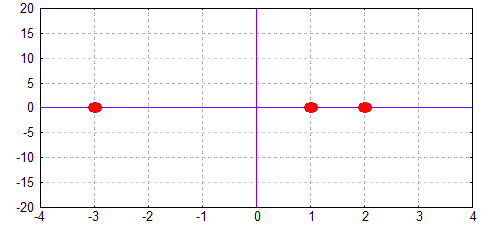
|
 |
Verhalten für große |x|
bestimmen |
|
Jetzt müssen wir uns überlegen, wie die Funktion für große x verläuft.
Die Funktion f(x)=(x–1)(x–2)(x+3)
ist eine Funktion dritten Grades,
was man erkennt, wenn man den Funktionsterm ausmultipliziert, oder
einfacher,
indem man das x–Glied in den Klammern multipliziert. Man erhält x3.
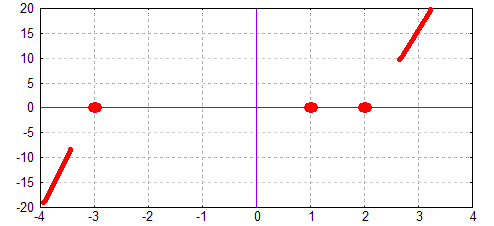
Für große |x|, d.h. für große x oder große negative x, verläuft eine
Polynomfunktion
immer so, wie ihr größtes Glied, also wie die Funktion g(x)= x3.
Diese Funktion verläuft von "links unten" nach "rechts oben".
Wir zeichnen diese Erkenntnis in das Koordinatensystem ein:
|
 |
Funktion zeichnen und Lösung
bestimmen |
|
Nun verbinden wir die beiden Teilstücke des Graphen miteinander. An den
Nullstellen wechselt die Funktion jeweils das Vorzeichen, d.h. sie
kreuzt die x-Achse:
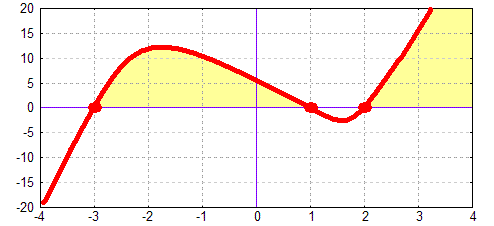
Nun können wir vom Bild ablesen, wann die Funktion f(x)=(x–1)(x–2)(x+3)
größer als Null ist, und somit die Ungleichung (x–1)(x–2)(x+3)>0
wahr ist:
Die Funktion f(x) ist in den Intervallen (–3,1) und (2,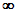 )
größer Null, )
größer Null,
und somit hat die Ungleichung die Lösungsmenge:
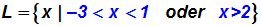 |
| |
|