Lösungsweg für den Fall:
Ungleichung hat
mehrfache Nullstellen |
 |
Mehrfache Nullstellen |
|
Im vorigen Fall hatten wir
Polynomungleichungen untersucht, die in
Linearfaktoren (x–a) mit ( )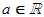
zerlegt waren. Nun wollen wir den Sonderfall
betrachten, dass mindestens ein Linearfaktor mehrfach vorkommt.
Beispiel:
(x–1)2 · (x–5)3
> 0
|
|
|
Deuten der Ungleichung als
Funktion |
|
Wir schon im vorigen Fall deuten wir die linke Seite der
Polynomungleichung als Funktion:
|
|
|
Einzeichnen der Nullstellen |
|
Die Nullstellen der Funktion
f(x)=(x–1)2·(x–5)3
können wir wieder direkt
vom Funktionsterm ablesen. Die Funktion ist gleich Null, wenn einer der
Faktoren gleich Null ist, also wenn x=1 oder x=5.
Wir zeichnen die Nullstellen in ein Koordinantensystem ein:
|
|
|
Verhalten für große |x|
bestimmen |
|
Das Verhalten für große x bestimmt man wie im vorigen Fall:
Jetzt müssen wir uns überlegen, wie die Funktion für große x verläuft.
Die Funktion
f(x)=(x–1)2·(x–5)3 ist eine Funktion
fünften Grades, denn
wenn man ein Polynom 2.Grades mit einem Polynom 3.Grades multipliziert,
dann erhält man ein Polynom 5.Grades (mehr dazu im Kurs "Polynome").
Für große |x|, d.h. für große x oder große negative x, verläuft eine
Polynomfunktion
immer so, wie ihr größtes Glied, also im Beispiel wie die Funktion g(x)= x5.
Diese Funktion verläuft von "links unten" nach "rechts oben".
Wir zeichnen diese Erkenntnis in das Koordinatensystem ein:
|
|
|
Verhalten an den Nullstellen bestimmen |
|
Das verbinden der Teilstücke ist nun etwas komplizierter, als im vorigen
Fall.
Die Nullstelle x=1 ist eine doppelte Nullstelle. Wir wissen aber, dass
eine Funktion
ihr Vorzeichen an einer Nullstelle nicht wechselt, wenn die
Nullstelle eine 2-fache,
4-fache, 6-fache, ... Nullstelle ist, also eine Nullstelle mit gerader
Vielfachheit.
Wir zeichnen daher ein, dass die Funktion bei x=1 ihr Vorzeichen
nicht wechselt:
Die Nullstelle x=5 ist eine dreifache Nullstelle. Wir wissen aber, dass
eine Funktion
ihr Vorzeichen an einer Nullstelle wechselt, wenn die
Nullstelle eine 1-fache,
3-fache, 5-fache, ... Nullstelle ist, also eine Nullstelle mit ungerader
Vielfachheit.
Wir zeichnen daher ein, dass die Funktion bei x=5 ihr Vorzeichen ändert:
Nun können wir vom Bild ablesen, wann die Funktion
f(x)=(x–1)2·(x–5)3
größer als Null ist, und somit die Ungleichung
(x–1)2·(x–5)3>0
wahr ist:
Die Funktion f(x) ist nur im Intervall (5, )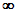
größer Null:
Und somit hat die Ungleichung die Lösungsmenge:
 |
| |
|