Die Umkehrfunktion
der Potenzfunktion |
 |
Erlaubte Umformungen:
Äquivalenzumformungen |
|
Wir haben am Anfang des Kapitels die Äquivalenzumformungen für
Ungleichungen
aus dem Kapitel Ungleichungen wiederholt.
Das Anwenden einer streng-monoton
steigenden Funktion ist zum Beispiel eine Äquivalenzumformung. Beispiel:
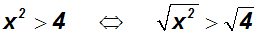
Natürlich darf der Definitionsbereich nicht verkleinert werden und es
darf kein
undefinierter Ausdruck entstehen. Dies ist hier jedoch nicht der Fall,
und daher
handelt es sich um eine Äquivalenzumformung.
|
 |
Sinnvolle Umformungen:
Umkehrfunktion anwenden |
|
Im Kurs Ungleichungen haben wir aber noch eine zweite Sache über das
Anwenden
einer streng monotonen Funktion gelernt:
Wenn man eine beliebige streng-monotone Funktion auf eine
Ungleichung anwendet,
dann ist dies zwar eine Äquivalenzumformung (vorausgesetzt kein
undefinierter
Ausdruck entsteht und der Definitionsbereich wird nicht
eingeschränkt),
jedoch hilft uns dies nicht die Ungleichung zu lösen. Man
muß eine ganz bestimmte
streng-monotone Funktion anwenden, nämlich die
Umkehrfunktion
der Funktion,
die in der Ungleichung beseitigt werden soll.
|
 |
Die Umkehrfunktion der geraden
Potenzfunktion |
|
Für Potenzungleichungen mit geraden Exponenten bedeutet dies:
Um eine Potenzungleichung mit geradem Exponenten
zu lösen,
muß man auf beiden Seiten der Ungleichung die
Wurzel ziehen (radizieren),
denn die
Wurzelfunktion ist die Not-Umkehrfunktion der
Potenzfunktion.
Der Name "Not-Umkehrfunktion" deutet an, dass eine gerade Potenzfunktion
keine Umkehrfunktion hat. Die Wurzelfunktion ist nämlich nur die
Umkehrfunktion
der eingeschränkten Potenzfunktion ist (d.h. einer geraden
Potenzfunktion, deren
Definitionsbereich auf nicht-negative Zahlen einschränkt wurde). Es gilt
aber:
Bei Potenzungleichungen mit geraden Exponenten reicht die
Not-Umkehrfunktion
(d.h. die Wurzelfunktion) aus, um die Potenzungleichung zu lösen,
denn man
kann einen Trick (ein bestimmtes Wurzelgesetz) anwenden. Wir
erklären aber
erst im Kapitel 2 ausführlich, wie dies funktioniert:
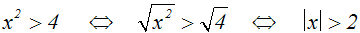
|
 |
Die Umkehrfunktion der
ungeraden Potenzfunktion |
|
Bei Potenzungleichungen mit ungeraden Exponent
hilft die Wurzelfunktion
als
Not-Umkehrfunktion in Verbindung mit dem "Trick" nicht aus, denn es
gilt:
Das Anwenden der Wurzelfunktion auf eine ungerade
Potenz in einer Ungleichung
kann zum Verlust von Lösungen führen oder zu
undefinierten Ausdrücken, wie
im folgenden Beispiel (die Wurzel aus einer
negativen Zahl ist ja nicht definiert):

Daher müssen wir uns überlegen, wie die tatsächliche Umkehrfunktion der
ungeraden Potenzfunktion lautet:
Die Umkehrfunktion der ungeraden Potenzfunktion f(x)=xn
(n=ungerade) lautet:
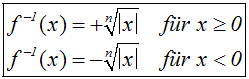
Wie man sieht, wird die Umkehrfunktion einer ungeraden Potenzfunktion
meist
nicht in der Form einer einzigen Formel angeben. Dies ist vielleicht
ungewohnt,
aber unbedeutend. Man nennt so eine Funktion übrigens "stückweise
definiert".
|
 |
Die "echte" Umkehrfunktion
ungeraden Potenzfunktion |
|
Will man die Umkehrfunktion der ungeraden Potenzfunktion nicht stückweise definieren,
sondern in einer
einzigen Formel,
so erhält man die folgende Formel, die wir
am Ende von Kapitel 2 erklären werden:
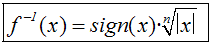
Weil diese Funktion recht kompliziert aussieht, wird sie meist nicht
angewendet,
sondern man benutzt die stückweise definierte Umkehrfunktion. Wir werden
uns
dieser Praxis beugen, aber am Ende von Kapitel 2 trotzdem zwei Beispiele
angeben.
|
|
|
|