x² < a
(a sei nicht-negativ) |
 |
Lösungsweg |
|
Gegeben ist die Potenzungleichung mit geradem Exponent:
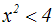
Beide Seiten der Ungleichung sind nicht-negativ (positiv oder Null): Die
linke
Seite der Ungleichung ist nicht-negativ, weil Quadrate immer
nicht-negativ sind.
Daher schränken wir den Definitionsbereich nicht ein, wenn wir auf
beiden
Seiten der Ungleichung die Wurzel ziehen. Da die Wurzelfunktion auch
noch
streng monoton steigend ist, ist das Wurzelziehen hier eine
Äquivalenzumformung:
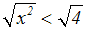
Auf der linken Seite wenden wir jetz das folgende Wurzelgesetz an: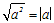
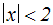
Wir lösen diese Betragsungleichung und erhalten die Lösung:
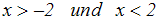 |
| |
|