x³ > a
(a nicht-negativ) |
 |
Lösungsweg |
|
Gegeben ist die Potenzungleichung mit
ungeradem Exponent der Form:
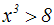
Wir machen eine
Fallunterscheidung, um die Ungleichung zu lösen:

Weil im Fall 2 die Lösungsmenge leer ist, besteht die Lösungsmenge
der Ungleichung
nur aus den Lösungen des Falles 1: L={x|x>2}.
|
 |
Praktisches Vorgehen in der
Schule |
|
Gegeben ist wieder die Potenzungleichung:
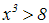
Meist wird diese Potenzungleichung ohne Fallunterscheidung gelöst.
Dies ist zwar total falsch, führt aber zufälligerweise zum richtigen
Ergebnis.
Zuerst ziehen wir auf beiden Seiten die dritte Wurzel:
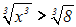
Dann wenden wir auf der linken Seite das folgende Wurzelgesetz an:
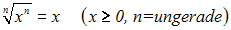
Wir erhalten
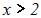
Erkärung:
Zuerst haben wir radiziert, wodurch der Definitionsbereich eingeschränkt
wurde
und Lösungen verloren gingen. Dann haben wir ein Wurzelgesetz
angewendet,
dass eigentlich nur für nicht-negative x gilt. Dadurch hat sich der
Definitionsbereich
wieder vergrößert. Beide Fehler, d.h. die Verkleinerung und
anschließende
Vergrößerung des Definitionsbereiches, heben sich also gegenseitig auf.
|
| |
|