x³ < –a
a sei positiv,
d.h.
–a sei negativ |
 |
Vorbemerkung |
|
Wir zeigen zwei Methoden, wie man die Potenzungleichung löst.
Die Methode 1 ist dabei einfacher und kürzer.
|
 |
Lösungsmethode 1 |
|
Gegeben ist eine Potenzungleichung mit ungeradem Exponent der Form:
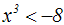
Wir machen eine Fallunterscheidung, um
die Ungleichung zu lösen:

|
 |
Lösungsmethode 2 |
|
Gegeben ist eine Potenzungleichung mit ungeradem Exponent der Form:
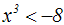
Wir machen eine Fallunterscheidung, um
die Ungleichung zu lösen:

|
| |
|