Alternatives
Lösungsverfahren
für Theoretiker:
Die echte
Umkehrfunktion
anwenden |
 |
Anwenden der "echten"
Umkehrfunktion |
|
Wie im Kapitel I erwähnt, kann man nicht
nur die stückweise definierte
Umkehrfunktion der ungeraden Potenzfunktion anwenden, sondern auch die
geschlossen
definierte Umkehrfunktion. Die Umkehrfunktion einer ungeraden
Potenzfunktion xn lautet:
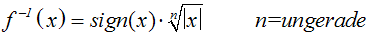
Wir haben diese Umkehrfunktion im Kurs
Potenzfunktionen
hergeleitet.
Wir zeigen daher hier nur noch Beispiele, wie man die
Umkehrfunktion
bei ungeraden Potenzungleichungen anwendet.
|
 |
Beispiel 1 |
|
Gegeben ist wieder eine Potenzungleichung mit ungeradem Exponent:
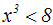
Wie gesagt hat eine ungerade Potenzfunktion f(x)=xn die Umkehrfunktion:
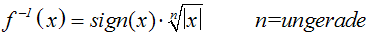
Im Falle der Kubikfunktion f(x)=x3 lautet die Umkehrfunktion daher
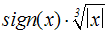 . .
Dabei ist sign(x) die Vorzeichenfunktion, die für negative Werte den
Wert –1 hat,
und ansonsten gleich 1 ist.
Wir wenden diese Funktion an. Da sie für alle x definiert ist, führt sie
zu keinem undefinierten
Ausdruck. Da sie auch streng monoton steigend ist, ist es auch eine
Äquivalenzumformung:
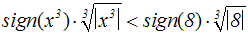
Auf der linken Seiten der Ungleichung heben sich Kubikfunktion und
Umkehrfunktion auf:
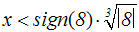
Die rechte Seite der Ungleichung kann man berechnen. Der Wert von
sign(8) ist 1:
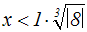
Der Betrag von 8 ist 8:
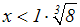
Wir erhalten die Lösung:
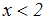
|
 |
Beispiel 2 |
|
Gegeben ist wieder eine Potenzungleichung mit ungeradem Exponent:
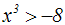
Wie gesagt hat eine ungerade Potenzfunktion f(x)=xn die Umkehrfunktion:
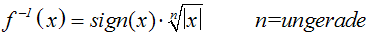
Im Falle der Kubikfunktion x3 lautet die Umkehrfunktion daher
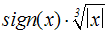 . .
Dabei ist sign(x) die Vorzeichenfunktion, die für negative Werte den
Wert –1 hat,
und ansonsten gleich 1 ist.
Wir wenden diese Funktion an. Da sie für alle x definiert ist, führt sie
zu keinem undefinierten
Ausdruck. Da sie auch streng monoton steigend ist, und der
Definitionsbereich nicht
eingeschränkt wird, ist das Anwenden der Funktion auch eine
Äquivalenzumformung:
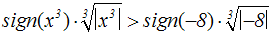
Auf der linken Seiten der Ungleichung heben sich Kubikfunktion und
Umkehrfunktion auf:
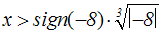
Die rechte Seite der Ungleichung kann man berechnen. Der Wert von
sign(–8) ist –1:
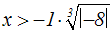
Der Betrag von –8 ist 8:
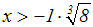
Wir erhalten die Lösung:
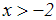 |
| |
|