 |
Schritt 1: Die
Fallunterscheidung |
|
Das Lösen einer Potenzungleichung mit
ungeradem Exponenten beginnt
grundsätzlich mit einer Fallunterscheidung. Dabei unterscheidet man
zwischen den zwei Fällen: x 0
und x<0. 0
und x<0.
Dann wird die Potenzungleichung für beide Fälle seperat gelöst.
Für jeden Fall gibt es natürlich auch eine Lösungsmenge
|
 |
Schritt 2: Umkehrfunktion
anwenden |
|
Jetzt wendet man die Umkehrfunktion an:
Sind beide Seiten der Ungleichung positiv, so wendet man die
in Kapitel 1 erwähnte "Umkehrfunktion für positive x" an:
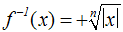
Sind beide Seiten der Ungleichung negativ, so wendet man die
in Kapitel 1 erwähnte "Umkehrfunktion für negative x" an:
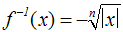
|
 |
Schritt 3: Vereinigungsmenge
bilden |
|
Am Ende bildet man die Vereinigungsmenge
der beiden Lösungsmengen.
Dies ist dann die Lösungsmenge der Potenzungleichung. |
| |