|
|
|
Hinweis:
Diese Erklärung gibt es auch als Video |
|
|
|
Wir wollen anhand eines Beispiels zeigen, wie man den
Graphen der allgemeiner Form ermitteln kann, ohne eine
Wertetabelle aufzustellen. Dazu
wandeln wir die allgemeine quadratische Funktion in die Verschiebeform um. Gegeben ist
die allgemeine quadratische Gleichung: |
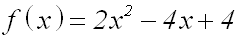 |
|
|
Zuerst klammern wir den Faktor des quadratischen Gliedes
aus: |
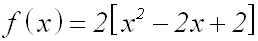 |
|
|
Hinter den ersten beiden Gliedern in der Klammer lassen
wir nun einen Abstand: |
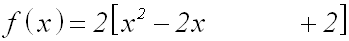 |
|
|
Nun bilden wir die quadratische Ergänzung zu den ersten
beiden Gliedern in der Klammer. Die quadratische
Ergänzung ist 1. Diese addieren wir. Natürlich müssen
wir gleichzeitig 1 subtrahieren, damit sich die
Funktionsgleichung nicht ändert: |
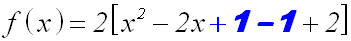 |
|
|
Die ersten drei Glieder der Klammer werden nun zu einem
Binom: |
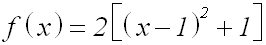 |
|
|
Jetzt multiplizieren wir die äußere Klammer aus. Dadurch
erhalten wir die Verschiebeform: |
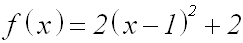 |
|
|
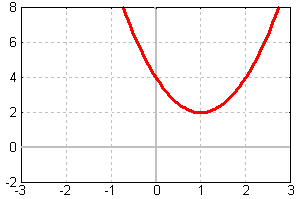
Anhand der Verschiebform können wir nun sagen, wie der
Graph der Funktion aussieht. Es ist eine Normalparabel
die um den Faktor 2 gestreckt ist. Sie ist um 2
Einheiten nach oben verschoben, und um 1 Einheit nach
rechts: |
 |
|