Eine quadratische Funktion hat entweder zwei, eine oder
keine Nullstellen.
1.Die
quadratische Funktion hat zwei Nullstellen
Falls sie zwei Nullstellen hat, dann kann man den
Scheitelpunkt leicht berechnen.
Der Scheitelpunkt
liegt dann nämlich zwischen den beiden Nullstellen,
was man am folgenden Bild leicht erkennen kann:
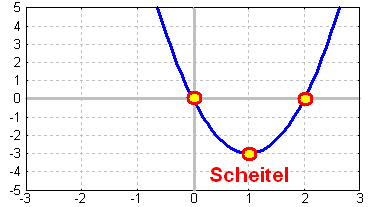
Bild: Die quadratische Funktion f(x)=3x2–6x. |
Die quadratische Funktion im Bild hat die beiden Nullstellen
x=0 und x=2.
Der arithmetische Mittelwert von 0 und 2 ist die Zahl 1.
Der Scheitel liegt also bei x=1
Die y-Koordinate des Scheitels erhält man übrigens
dadurch, dass man die berechnete
x-Koordinate (hier x=1) in die gegebene
Funktionsgleichung (hier: f(x)=3x2–6x)
einsetzt.
Im Beispiel ergibt sich die y-Koordinate y = –3
für den Scheitelpunkt, was man auch im Bild sieht.
2.Die
quadratische Funktion hat nur eine Nullstelle
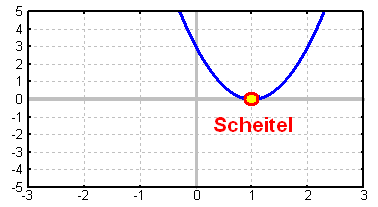
Falls eine quadratische Funktion nur eine Nullstelle
hat, dann sind Nullstelle und Scheitelpunkt identisch:
 |