|
|
Falls die quadratische Funktion keine Nullstelle hat,
und man nicht die
Methode der quadratischen Ergänzung benutzen will,
um den Scheitel zu berechnen
(manche Leute können sich die Methode der quadratischen
Ergänzung nicht merken),
dann gibt es noch ein zweites Verfahren, um den Scheitel
zu bestimmen:
|
x-Koordinate des
Scheitel berechnen
|
Wir wollen das Verfahren an einem Beispiel
erklären.
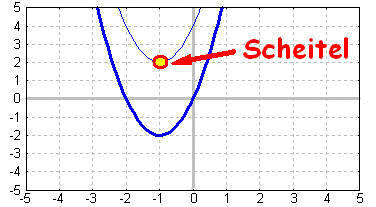
Gegeben sei die quadratische Funktion, die keine
Nullstelle hat
(im Bild unten ist es der obere, dünne Graph):
:
f(x) = 2x²+4x+4
Wir lassen nun das Absolutglied wegfallen. Die
x-Koordinate des Scheitels ändert sich dadurch
nicht, denn das Weglassen des Absolutgliedes
bewirkt nur eine vertikale (senkrechte) Verschiebung:
f(x) = 2x²+4x
Wir berechnen die Nullstellen der
Funktion, indem wir sie gleich Null setzen
Dies ist sehr einfach, denn weil jetzt das
Absolutglied fehlt, können wir x ausklammern,
und brauchen nicht die umständliche
Lösungsformel für quadratische Gleichungen
benutzen:
x(2x+4)=0
Ein Produkt ist genau dann gleich Null, wenn
mindestens ein Faktor gleich Null ist.
Folglich lautet die erste Lösung x=0 und die andere erhält man, wenn
man die Klammer
gleich Null setzt.Wir erhalten die beiden
Lösungen:
x=0 oder x= –2
Der Scheitel liegt nun (wie wir bereits
wissen) zwischen den
beiden Nullstellen,
also zwischen dem Ursprung und der anderen
Nullstelle.
Im Beispiel liegt der Scheitel zwischen 0 und
–2, also bei x= –1.
|
|
y-Koordinate des
Scheitels berechnen
|
Nun müssen wir nur noch die y-Koordinate des
Scheites berechnen.
Dazu setzen wir die ermittelte x-Koordinate des
Scheitels (x= –1) in die
ursprüngliche Gleichung ein.
f(x) = 2(–1)²+4(–1)+4
= 2
| Der Scheitel liegt also bei (–1/2). |
|
|
|