Im letzten Kapitel haben wir die quadratische Grundfunktion kennengelernt.
Multipliziert man die quadratische Grundfunktion f(x)=x²  mit einem Faktor a,
so erhält man eine reinquadratische Gleichung  f(x)=a·x². Beispiele:
  


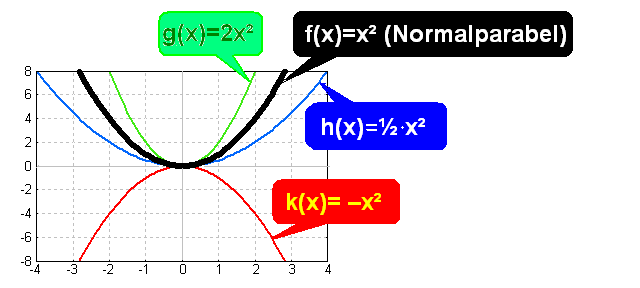
Der Faktor a bewirkt folgende Veränderung (siehe Bild):
Eine Streckung, wenn a größer als 1 ist 
 Eine Stauchung, wenn der Betrag von a zwischen 0 und 1 liegt 
 Eine Spiegelung, wenn a negativ ist  

Reinquadratische Funktionen
Die Menge aller gestreckten, gestauchten und gespiegelten Normalparabeln bilden
(zusammen mit der Normalparabel) die Menge der "Reinquadratischen Funktionen".
Der Name rührt daher, weil reinquadratische Funktionen nur ein quadratisches Glied haben.

Später werden wir auch quadratische Funktionen kennenlernen, die zusätzlich ein Linearglied
und/oder ein Absolutglied haben, wie z.B. die Funktion f(x)= 2x²+3x+4