1.Das Problem:  

Gegeben ist eine reinquadratische Gleichung:

Wir wollen beweisen, daß die Parallel-Verschiebung
der Parabel um u Einheiten nach links einen Graphen
ergibt, der die folgende Funktionsgleichung hat:

 

2.Der Beweis:

Die Koordinaten eines Punktes auf der Originalparabel nennen wir:
 
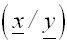
Die Koordinaten eines Punktes auf der verschobenen Parabel nennen wir:

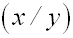
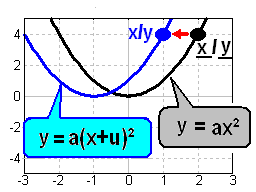
Nun betrachten wird den Zusammenhang zwischen den Koordinaten eines Originalpunktes
und des um u Einheiten nach links verschobenen Punktes. Die y-Koordinate eines
verschobenen Punktes ist identisch mit der y-Koordinate des Originalpunktes:

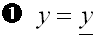
Die x-Koordinate des nach links verschobenen Punktes (x/y) ist
um u Einheiten kleiner als die x-Koordinate des Originalpunkte (x/y):

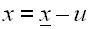
Wir stellen die Gleichung nach x um, und erhalten:

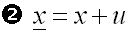
Die Funktionsgleichung der Originalparabel ist:

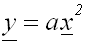
In dieser Funktionsgleichung ersetzen wir x und y
mit Hilfe der aufgestellen Gleichungen 1 und 2:

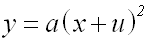
Dies ist die Funktionsgleichung, die wir beweisen wollten.