1.Das Problem:  

Gegeben ist eine reinquadratische Gleichung:

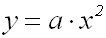
Wir wollen beweisen, daß die Parallel-Verschiebung
der Parabel um v Einheiten nach oben einen Graphen
ergibt, der die folgende Funktionsgleichung hat:

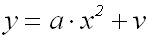
Es sei angemerkt, daß eigentlich kein Beweis nötig ist,
denn man kann diese Funktionsgleichung,
d.h. die Funktionsgleichung der verschobenen Parabel,
auch der Anschauung entnehmen.
 

2.Der Beweis:

Die Koordinaten eines Punktes auf der Originalparabel nennen wir:
 
Die Koordinaten eines Punktes auf der verschobenen Parabel nennen wir:

Nun betrachten wird den Zusammenhang zwischen den Koordinaten eines Originalpunktes und des um v Einheiten nach oben verschobenen Punktes. Die x-Koordinate eines verschobenen Punktes ist identisch mit der x-Koordinate des Originalpunktes:

Die y-Koordinate des nach oben verschobenen Punktes (x/y) ist um v Einheiten größer als die y-Koordinate des Originalpunkte (x/y):

Wir stellen die Gleichung nach y um, und erhalten:

Die Funktionsgleichung der Originalparabel ist:

In dieser Funktionsgleichung ersetzen wir x und y mit Hilfe der aufgestellen Gleichungen 1 und 2:

Wir addieren v auf beiden Seiten:

Dies ist die Funktionsgleichung, die wir beweisen wollten.