|
|
| Bis jetzt haben wir reinquadratische
Funktionen f(x)= ax² betrachtet.
Sie haben als Graphen eine Parabel.
Nun wollen wir diese Parabeln
parallelverschieben, und herausfinden
welche Funktionsgleichung eine
parallel-verschobene Parabel hat. |
|
 |
|
|
|
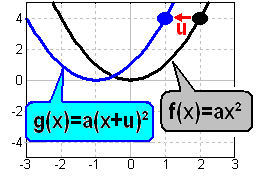
Verschiebung nach links
durch
Addition von u zum Argument
x |
Der Graph einer
reinquadratischen Funktion:
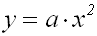
wird um u Einheiten nach
links parallel-verschoben,
sodass der Scheitel bei
(–u/0) lieg, im Beispiel bei
(–1/0).
Dann hat die verschobene
Parabel die
Funktionsgleichung:
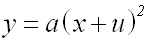
Achtung: Viele Schülern
erscheint es unlogisch, dass
durch
eine Addition eine
Verschiebung in Richtung des
negativen
Bereichs erfolgt. Daher
gibt es dazu ein Video mit
Zusatzerklärungen. |
|
|
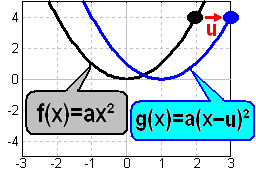 |
|
|
|
Verschiebung nach rechts
durch
Subtraktion von u vom
Argument x |
Der Graph einer
reinquadratischen Funktion:
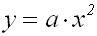
wird um u Einheiten nach
rechts parallel-verschoben,
sodass der Scheitel bei (u/0)
lieg, im Beispiel bei (1/0).
Dann hat die verschobene
Parabel die
Funktionsgleichung:
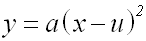
|
|
|
 |
|
|
|
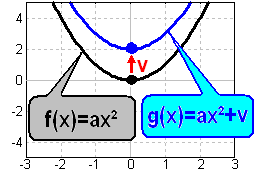
Verschiebung nach oben
durch Addition von v |
Der Graph einer
reinquadratischen Funktion:
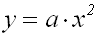
wird um v Einheiten nach
oben parallel-verschoben,
so dass der Scheitel bei (0/v)
lieg, im Beispiel bei (0/2).
Dann hat die verschobene
Parabel die
Funktionsgleichung:
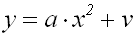
|
|
|
 |
|
|
|
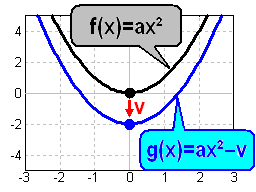
Verschiebung nach unten
durch Subtraktion von v |
Der Graph einer
reinquadratischen Funktion:
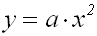
wird um v Einheiten nach
unten parallel-verschoben,
so dass der Scheitel bei
(0/–v) lieg, im Beispiel bei
(0/–2).
Dann hat die verschobene
Parabel die
Funktionsgleichung:
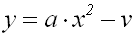
|
|
|
|
|
|