|
Was ist eine Approximation? |
 |
Was ist ein Approximation? |
|
In diesem Kurs wollen wir zeigen, wie man eine beliebige Funktionen
durch eine Polynomfunktion approximiert (annähert). Wir wollen also
zu einer Funktion eine Polynomfunktion ermitteln, die zumindest
in einen gewissen Bereich fast die gleichen Funktionswerte hat.
|
 |
Beispiel |
|
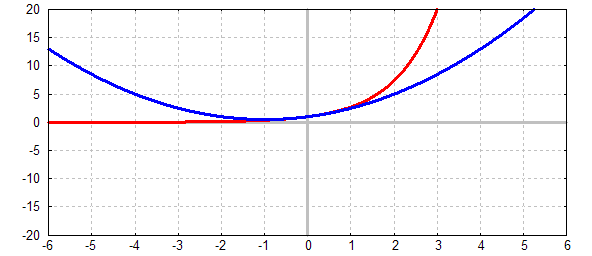
Im Bild sehen wir die natürliche Exponentialfunktion (rot) und eine
Polynomfunktion (blau), welche die Exponentialfunktion approximiert.
Die Stelle, in deren Umgebung die Funktion approximiert werden soll,
nennt man Entwicklungsstelle. In unserem Beispiel ist dies die Stelle
x=0.
Die Näherung (Approximation) ist zwischen –1 und 1 sehr gut,
und wird danach schnell schlechter:
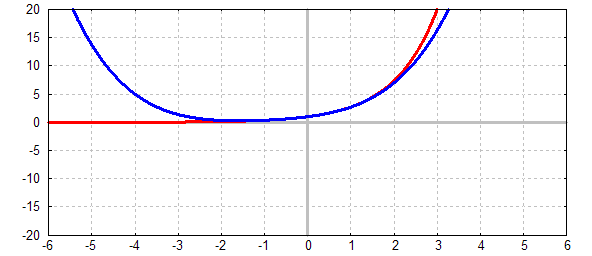
Um die Approximation zu verbessern, muß meist ein Polynom höheren Grades
verwendet werden. Wir sehen: Die Approximation ist nun sogar zwischen –2
und 2
sehr gut, denn beide Funktionsgraphen stimmen fast überein:
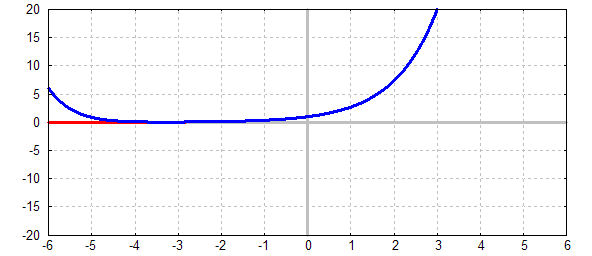
Wählt man ein Polynom mit noch höheren Grad, so wird die Approximation
der Funktion in der Regel immer besser:
In diesem Kurs lernen wir, wie man diese Polynome berechnet,
welche eine bestimmte Funktion möglichst gut approximieren.
Im Wesentlichen bedient man sich dazu der Methode von Taylor
(Brook Taylor, englischer Mathematiker, 1685-1731).
|
 |
Wozu approximiere ich
Funktionen? |
|
Es gibt verschiedene Gründe, um eine Funktion zu approximieren:
Nehmen wir an, ich habe eine komplizierte Funktion, die ich
integrieren soll. Dann kann ich die komplizierte Funktion durch
eine Polynomfunktion approximieren, und dann die Polynomfunktion
integrieren.
Um die Funktionswerte von Funktionen wie sin(x), cos(x), exp(x) usw.
zu erhalten, tippen wir zum Beispiel sin(30°) in den Taschenrechner ein
(früher benutzte man Tabellen). Aber woher weiß der Taschenrechner,
wie groß sin(30°) ist? Der Taschenrechner hat diese Werte nicht
gespeichert,
sondern er hat eine Approximation der Sinusfunktion gespeichert, nämlich
eine Polynomfunktion.
Ein weiteres Anwendungsgebiet ist z.B. die Lösung von
Differentialgleichungen.
|
 |
Was erwarte ich von einer
guten Approximation |
|
Von einer guten Approximation erwartet man zwei Dinge:
1. Gute Approximation, d.h. Funktion und Polynom sollen sich
in der Nähe der Entwicklungsstelle wenig
unterscheiden
2. Die Funktion soll in einem weitem Bereich um die
Entwicklungstelle
gut approximiert werden.
|
| |
|