Die Idee des
Taylorverfahrens |
 |
Die Idee des Taylorverfahrens |
|
Im vorigen Kapitel haben wir gesehen, dass die Approximation
durch
eine Schmiegeparabel (also durch ein Polynom 2.Grades) besser ist,
als eine Approximation durch eine Tangentengerade (Polynom 1.Grades).
Das liegt daran, weil bei der Schmiegeparabel zusätzlich
gefordert wird,
dass an der Entwicklungsstelle xe auch
die 2.Ableitung der Funktion
mit der 2.Ableitung des Polynoms übereinstimmt.
Das Taylorverfahren verallgemeinert diese Idee:
Man approximiert die Funktion durch ein Polynom
höheren Grades
und fordert, dass auch die höheren Ableitungen
von Funktion und
Polynom an der Entwicklungstelle xe
miteinander übereinstimmen.
Zum Beispiel kann man die Sinusfunktion durch ein Polynom 5.Grades
approximieren und fordern, dass die ersten 5. Ableitungen der
Sinusfunktion und des (Approximations)Polynoms übereinstimmen.
Die Praxis zeigt: Dadurch wird die Approximation der Funktion durch
das Polynom noch besser, als die Approximation durch eine
Schmiegeparabel.
|
 |
Beispiel |
|
Aufgabe:
Wir wollen die Sinusfunktion an der Stelle x=0 durch ein Polynom
5.Grades
approximieren und fordern daher, dass die ersten 5 Ableitungen der
Sinusfunktion und des Polynoms an der Entwicklungsstelle x=0
übereinstimmen.
Lösungsidee:
Wir bilden nacheinander die ersten 5 Ableitungen der Sinusfunktion,
und setzen sie
an der Stelle x=0 mit den zugehörigen fünf Ableitungen
des Polynoms gleich.
Lösungsweg:
Wir setzen Funktion und Polynom
an der Stelle x=0 gleich:
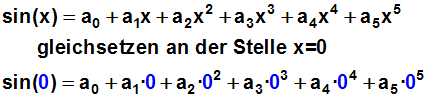
Weil (auf der rechten Seite der Gleichung) abgesehen vom ersten Term
alle Terme wegfallen, erhalten wir den ersten der gesuchten
Koeffizienten:
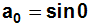
Jetzt bilden wir die 1.
Ableitung von Funktion und Polynom, und
setzen sie an der Stelle x=0 gleich:
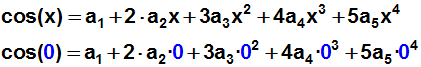
Weil wieder (auf der rechten Seite der Gleichung) abgesehen vom ersten
Term
alle Terme wegfallen, erhalten wir den nächsten gesuchten Koeffizienten:
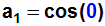
Anmerkung:
Der letzte Schritt (ableiten und x=0 setzen) wiederholt sich jetzt insgesamt fünfmal.
Jetzt bilden wir die 2.
Ableitung von Funktion und Polynom, und
setzen sie an der Stelle x=0 gleich:
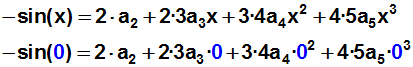
Weil wieder (auf der rechten Seite der Gleichung) abgesehen vom ersten
Term
alle Terme wegfallen, erhalten wir den nächsten gesuchten Koeffizienten:
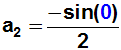
Jetzt bilden wir die 3.
Ableitung von Funktion und Polynom, und
setzen sie an der Stelle x=0 gleich:
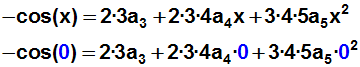
Weil wieder (auf der rechten Seite der Gleichung) abgesehen vom ersten
Term
alle Terme wegfallen, erhalten wir den nächsten gesuchten Koeffizienten:
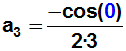
Jetzt bilden wir die 4.
Ableitung von Funktion und Polynom, und
setzen sie an der Stelle x=0 gleich:
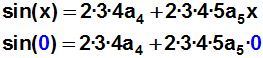
Weil wieder (auf der rechten Seite der Gleichung) abgesehen vom ersten
Term
alle Terme wegfallen, erhalten wir den nächsten gesuchten Koeffizienten:
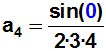
Jetzt bilden wir die 5.
Ableitung von Funktion und Polynom, und
setzen sie an der Stelle x=0 gleich:
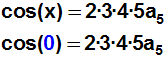
Weil wieder (auf der rechten Seite der Gleichung) abgesehen vom ersten
Term
alle Terme wegfallen, erhalten wir den nächsten gesuchten Koeffizienten:
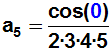
Zusammenfassung und vereinfachen der berechneten Koeffizienten:
Die berechneten Koeffizienten schreiben wir nochmal auf und
vereinfachen sie:
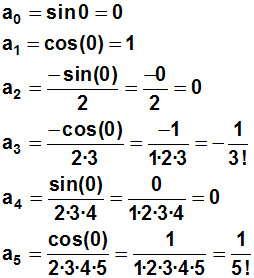
Berechnete Koeffizienten in den
gegebenen Ansatz einsetzen:
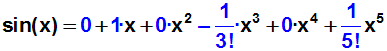
Da einige Summanden gleich Null sind ergibt sich die Lösung:
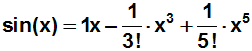 |
| |
|