Taylorreihen und Taylorpolynome

Taylorpolynome

Worum geht es:

Beweis der Taylorformel für die Entwicklungsstelle x=0

Gesucht

Wir wollen eine Funktion f(x) in der Nähe von x=0 durch ein Polynom approximieren, d.h. in der
Umgebung der Stelle x=0 soll die Funktion ungefähr gleich einem Polynom a₀+a₁x+a₂x²+ ... sein:

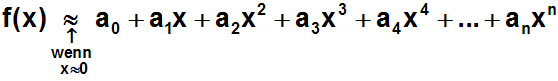
Um das gewünschte Polynom zu erhalten, müssen wir die Koeffizienten
a₀, a₁, a₂, a₃, a₄ , ... , a_n bestimmen. Dazu überlegen wir uns folgendes:

Schritt 0: a₀ bestimmen

Damit Funktion und Polynom in der Umgebung von x=0 ungefähr gleich sind, müssen sie an
der Stelle x=0 genau gleich sein (denn wenn sie schon für x=0 abweichen würden, würden sie in der
Umgebung von x=0 total abweichen). Daher setzen wir Funktion und Polynom an der Stelle x=0 gleich:

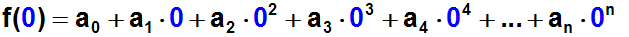
Außer dem ersten Glied der Reihe - nämlich a₀ -werden dadurch alle Glieder zu Null.
Somit können wir den Wert von a₀ ablesen:

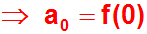
Nun ermitteln wir den nächsten Koeffizienten, und benutzen die ähnliche Idee:

Schritt 1: a₁ bestimmen

Wenn die Funktion und ihr Taylorpolynom für x=0 genau gleich sein sollen, dann müssen
auch die Ableitungen von Funktion und Polynom an der Stelle x=0 gleich sein. Wir bilden daher
auf beiden Seiten die Ableitung und setzen dann die Ableitungen (an der Stelle x=0) gleich:

Außer dem ersten Glied der Reihe - nämlich a₁ - werden dadurch alle Glieder zu Null.
Somit können wir den Wert von a₁ ablesen:

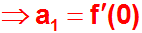
Nun ermitteln wir den nächsten Koeffizienten:

Schritt 2: a₂ bestimmen

Die Idee bei Schritt 2 ist fast die gleiche, wie bei Schritt 1: Wenn die Funktion und das Polynom
an der Stelle x=0 gleich sein sollen, dann müssen auch ihre höheren Ableitungen übereinstimmen.
Wir leiten also beide Seiten nochmal ab und setzen die Ableitungen (an der Stelle x=0) gleich:

Außer dem ersten Glied der Reihe - nämlich 2·a₂ - werden wieder alle Glieder zu Null.
Somit können wir den Wert von a₂ ablesen:

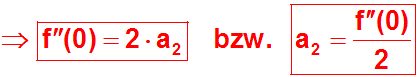
Schritt 3: a₃ bestimmen

Wie gesagt, wiederholt sich Schritt 1 immer wieder: Ableitungen bilden und an der Stelle x=0 gleichsetzen:

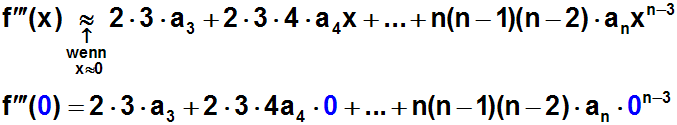
Außer dem ersten Glied der Reihe - nämlich 2·3·a₃- werden wieder alle Glieder zu Null.
Somit können wir den Wert von a₃ ablesen:

Schritt 4: a₄ bestimmen

Wie gesagt, wiederholt sich Schritt 1 immer wieder: Ableitungen bilden und an der Stelle x=0 gleichsetzen:

Außer dem ersten Glied der Reihe - nämlich 2·3·4·a₄ - werden wieder alle Glieder zu Null.
Somit können wir den Wert von a₄ ablesen:

Schritt n: a_n bestimmen

Nun kommen wir zum n-ten Schritt. Nach dem n-ten Ableiten setzen wir (so wie immer) für x die Zahl 0 ein:

Wir können den letzten gesuchten Koeffizienten nun ablesen, wenn wir die
letzte Gleichung nach a_n umstellen:

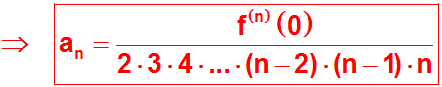
Letzter Schritt: Koeffizienten in die Formel einsetzen

Jetzt die in den vorigen Schritten berechneten Koeffizienten a₀, a₁, a₂, a₃ und a₄ in die gegebene Gleichung einsetzen:

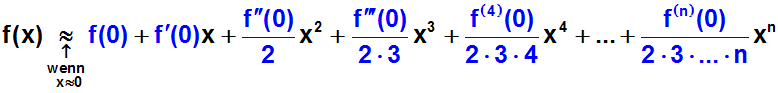Jetzt dividieren wir alle Terme durch 1. Dies ist erlaubt, denn die 1 ist das neutrale Element
der Division (d.h. es passiert nichts, wenn wir eine Zahl oder einen Bruch durch 1 dividieren):

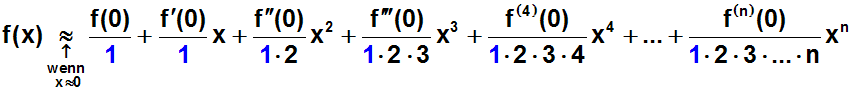
Dadurch können wir die sogenannte Fakultät-Schreibweise anwenden.
Eine kurze Wiederholung, wie die Fakultät definiert ist:

Man schreibt 1·2·3·4 als 4! (sprich: 4 Fakultät), oder allgemein: 1·2·3·...·n = n!
Außerdem legen wir fest: 0!=1 und 1!=1.

Die Formel vereinfacht sich zu:

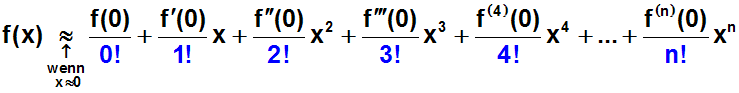
Nun sieht man auch schon das Bildungsgesetz: Die Ordnung der Ableitung entspricht dem Exponenten von x
und dem Argument der Fakultät. Damit dies auch für das erste Glied der Reihe gilt, definieren wir,
dass f(x) die "nullte Ableitung" von sich selbst ist: f(x) = f⁽⁰⁾(x).

Um noch mehr Schreibarbeit zu sparen, benutzen wir das Summenzeichen:

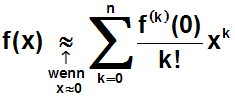
Man kann die Formel überprüfen: Setzt man für k nacheinander die Zahlen 0 bis n ein, so erhält man
wieder die "Formel ohne Summenzeichen".

Noch eine Anmerkung: In der vorletzten Formel läßt man 0! und 1! meist weg, denn beide sind ja gleich 1:

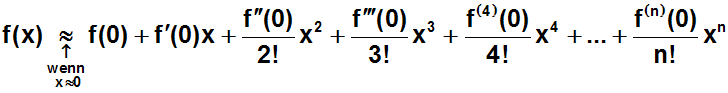
Ein Polynom dieser Form nennt man Taylorpolynom. Die Formel nennt man Taylorformel.

Die beiden letzten Formel sind die Formeln, die wir beweisen wollten.