Taylorreihe für
beliebige
Entwicklungsstelle |
 |
Worum geht es |
|
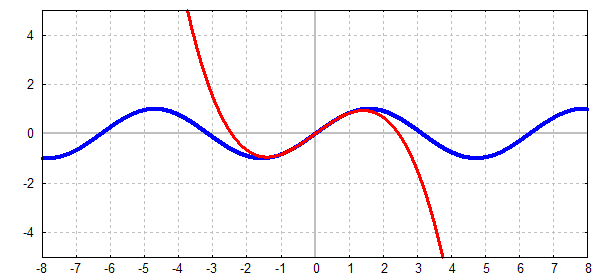
Bis jetzt haben eine Funktion (blau) durch ein Taylorpolynom
(rot)
in der Nähe von x=0 approximiert, indem wir
forderten, dass die Funktion
bzw.
ihre Ableitungen an der Stelle x=0
mit dem Taylorpolynom
übereinstimmten.
Die Approximation war an der Stelle x=0 genau und in der Umgebung
von
x=0
noch recht gut (natürlich auch abhängig vom Grad des Taylorpolynoms).
Je mehr man sich von der Stelle x=0 entfernte, desto ungenauer
wurde die
Approximation:
Nun kann es aber gewünscht sein, dass die Approximation
der Funktion stattdessen
an einer anderen, beliebigen Stelle
besonders gut
sein soll, z.B. an der Stelle xe (also z.B. bei x=3).
Dann muß man die Funktion an dieser Stelle xe "entwickeln",
d.h. man
fordert nicht,
dass die Funktion f(x) bzw. ihre Ableitungen
an der Stelle x=0 mit dem
Taylorpolynom
bzw. seinen Ableitungen
übereinstimmen, sondern an der
Stelle x=xe.
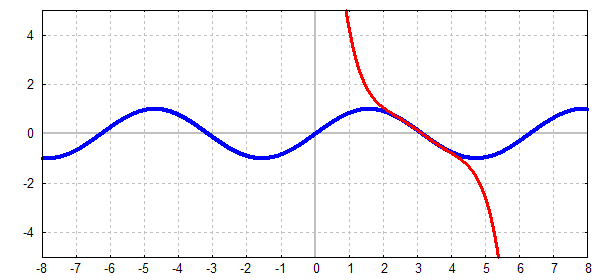
Dadurch wird die Funktion an der Stelle xe genau
approximiert (im Bild ist xe=3),
und auch
in der Umgebung der Stelle x=xe wird sie noch relativ gut
approximiert:
Das Taylorpolynom für eine beliebige Entwicklungsstelle xe
ergibt sich
dabei aus folgender Formel:
|
 |
Taylorformel für beliebige
Entwicklungsstelle |
|
Eine Funktion f(x) ist in der Nähe des Entwicklungspunktes xe
(also wenn x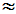 xe) xe)
ungefähr gleich ihrem Taylorpolynom, dass sich durch folgende Formel
bestimmt:
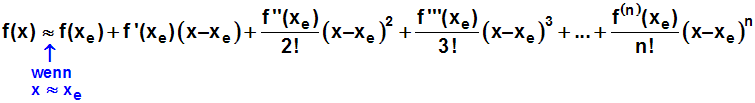
Oder in der Schreibweise mit dem Summenzeichen:
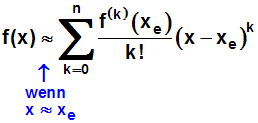
|
| |
|