Die Güte der
Approximation
wird durch viele
Glieder nur dann
besser, wenn man
sich im
Konvergenzbereich der
zugehörigen Reihe
befindet. |
 |
Erklärung |
|
Nun könnte man meinen, je mehr Glieder ein Taylorpolynom hat,
d.h. je höher sein Grad ist, desto genauer wird die Funktion
approximiert.
Das folgende Beispiel zeigt jedoch, dass dies oft nur für einen gewissen
Bereich gilt, den sogenannten Konvergenzbereich der zugehörigen Reihe:
Bildet man nämlich ein Taylorpolynom mit unendlich vielen Gliedern,
so erhält man eine Taylorreihe (wird im nächsten Kurs gemacht),
und nur im Konvergenzbereich dieser zugehörigen Taylorreihe
verbessert sich die Approximation mit steigender Anzahl der
Glieder.
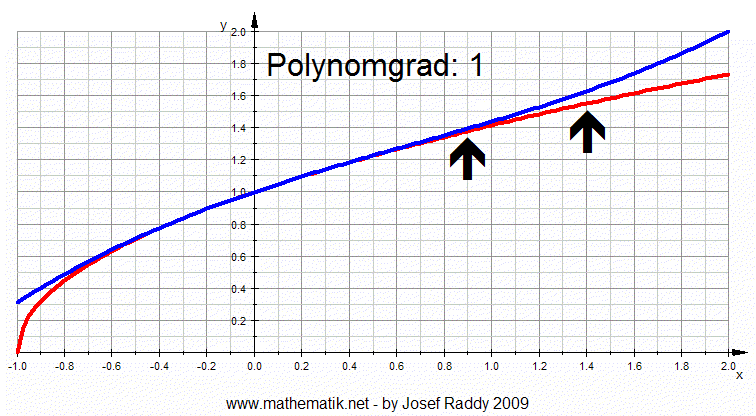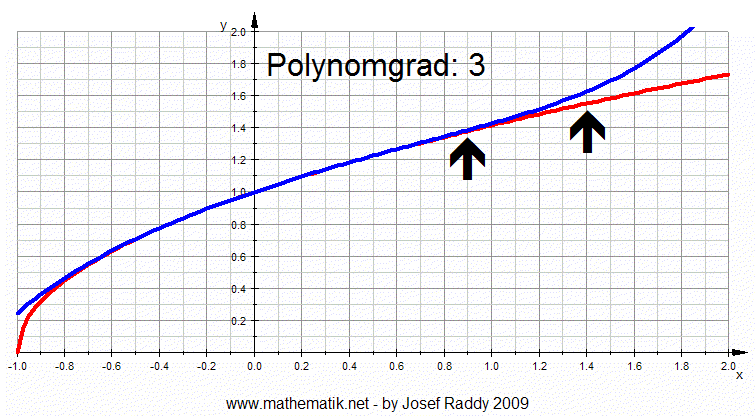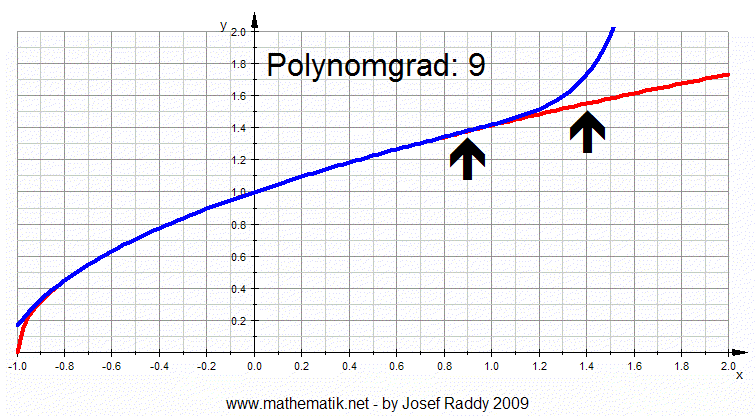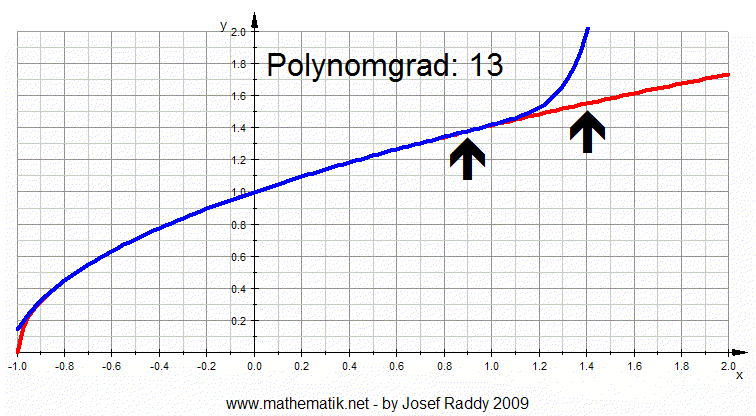
Im Beispiel (Animation unten) wird die rote Funktion
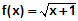 durch
Taylorpolynome (blau) im Bereich
(–1,1) desto besser approximiert, je größer der Grad des Polynoms wird
(beobachte die Stelle x=0.9).
Außerhalb des Bereichs (–1,1) wird die Approximation jedoch schlechter,
wenn der Grad des
Polynoms größer wird (gut zu erkennen, wenn man zum Beispiel die Stelle
x=1.4 beobachtet):
 |
|