Der Fehler bzw.
die Güte der
Approximation |
 |
Erklärung |
|
In diesem Kapitel wollen wir nun der Frage nachgehen, wie gut eine
Funktion
durch ein Taylorpolynom approximiert wird. Eine Approximation macht
nämlich
keinen Sinn, wenn man über die Güte der Approximation keine Aussage
machen kann.
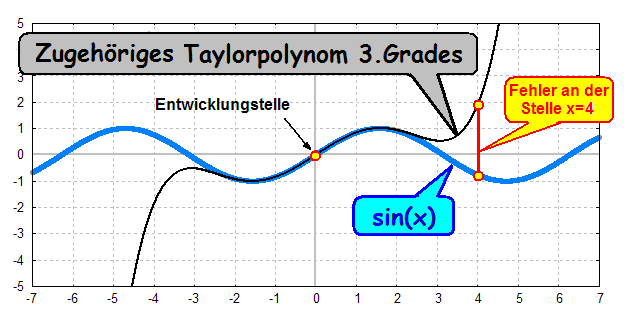
Im Bild sehen wir die Sinusfunktion (blau) und ihr Taylorpolynom
3.Grades (schwarz)
mit der Entwicklungstelle x=0. Außerdem ist die Differenz zwischen
Funktion und
dem Taylorpolynom für die Stelle x=4 eingezeichnet. Diese Differenz
nennt man Fehler:
Wie gesagt wollen wir in diesem Kapitel eine Formel angeben, mit der man
den Fehler
abschätzen kann. Zuerst wollen wir uns verdeutlichen, wovon der Fehler
abhängt:
| 1. |
Wie man im Bild oben sieht, ändert sich die Größe des
Fehlers, wenn ich eine andere
Stelle betrachtet. Bei x=2 ist der Fehler sehr gering (er ist im
Bild kaum sichtbar).
Bei x=4 ist der Fehler aber bereits sehr groß (fast 3 Kästchen).
|
| 2. |
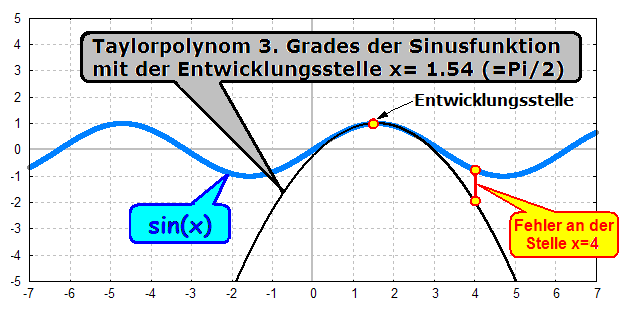
Der Fehler für eine bestimmte Stelle (wie z.B. x=4) ändert
sich aber auch,
wenn ich für das Taylorpolynom eine andere Enwicklungsstelle
wähle.
Im Bild unten habe ich die Sinusfunktion wieder durch ein
Taylorpolynom
3.Grades approximiert, aber diesmal habe ich die Sinusfunktion
an der
Stelle x=1.54 entwickelt. Man sieht, dass der Fehler an der Stelle
x=4
wesentlich geringer
geworden ist (nur noch etwas mehr als 1 Kästchen): |
Zusammengefaßt kann man sagen: Der Fehler hängt von der Stelle x ab,
und von der Entwicklungstelle xe, an der ich die Funktion
entwickelt habe.
Auf der nächsten Seite geben wir eine Formel an (Formel von Lagrange),
mit der man diesen Fehler (in Abhängigkeit von x und xe)
abschätzen kann.
|
|
| |
|