Restformel von
Lagrange |
 |
Restgliedformel von Lagrange |
|
Eine Funktion f(x) mit dem Definitionsbereich [xe,x]
sei (n+1)-mal differenzierbar.
Dann gibt es eine Stelle c in (xe,x), sodass für den
Rest Rn(x,xe) gilt:
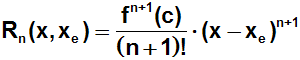
Somit gilt für die Funktion f(x):
 |
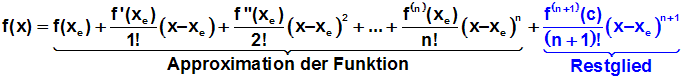Anmerkungen:
► n ist dabei der Grad des
Taylorpolynoms und xe
ist die Entwicklungsstelle.
► Das letzte Glied des Polynoms wird als Restglied bezeichnet,
oder als Rest.
► Beachte: Es ist nicht möglich, mit der Formel den Fehler an der Stelle x
zu berechnen,
denn die Stelle c ist unbekannt und weder mit der Formel noch sonstwie berechnet werden.
Der Satz
sagt
lediglich, dass eine Stelle c existiert, an welcher die
Berechnungsformel gilt.
Anmerkungen zu anderen Schreibweisen:
► Statt c schreibt man auch oft
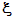(gesprochen: Xi, griechischer Buchstabe).
► Die Entwicklungsstelle wird statt
xe oft mit
x0 bezeichnet (manchmal
auch mit a, selten mit c).
► Das Restglied Rn(x,xe)
wird meist nur Rn(x)
genannt, was eigentlich etwas ungenau ist,
denn der Rest ist auch von der Entwicklungsstelle xe
abhängig (d.h. ist Funktion von ihr).
Wenn aber klar ist, wo die Funktion entwickelt wurde,
schreiben auch wir meist nur Rn(x).
► Das Restglied Rn(x,xe)
müßte eigentlich sogar R(x,xe,n)
geschrieben werden,
weil der Rest auch von n abhängig ist, jedoch schreibt
man das n meist in den Index.
► Das Restglied Rn(x,xe)
müßte eigentlich sogar R(x,xe,n,f)
geschrieben werden,
weil der Rest auch davon abhängig ist, welche Funktion
man betrachtet. Aber
diese Schreibweise ist noch seltener als es die vorige
schon ist.
|
|
|
Die Formel für die Abschätzung
des Fehlers: |
|
Wie soeben die Formel von Lagrange kennengelernt:
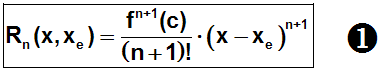
Wie gesagt, kann man mit der Formel den Fehler nicht berechnen, denn c
ist unbekannt.
Man kann aber aus ihr eine Formel herleiten, mit der man in den meisten
Fällen einen
Höchstwert angeben kann, den der Fehler R(x,xe)
nicht übersteigen wird. Zunächst einmal
bestimmen wir den Betrag des Fehlers. Dabei benutzen wir
den Satz: c=a·b => |c|=|a|·|b|
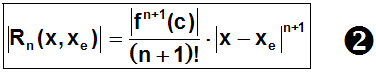
Jetzt schätzt man ab, wie groß der Ausdruck |f n+1 (c)| im
Intervall (xe,x) maximal werden kann:
Man berechnet den größten Wert, den der Ausdruck
|f n+1 (x)| im Intervall (xe,x)
annimmt,
und nennt diesen Maximalwert
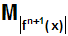 . Weil auch c (laut dem
Satz von Lagrange) im
Intervall (xe,x) liegt, kann
|f n+1(c)| diesen Wert logischerweise nicht überschreiten,
d.h. es gilt:
 .
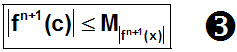Einsetzen der letzten Formel (3) in die vorletzte Formel (2) ergibt die
Abschätzung:
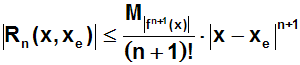
Auf den folgenden Seiten erklären wir anhand von Beispielen, wie man die
Formel anwendet. |
| |
|