Fehler an der
Stelle x=5
bei der
Approximation
der Funktion
f(x)=e0.5x durch
ein Taylorpolynom
2. Grades mit der
Entwicklungsstelle
xe=e
(e=Eulersche Zahl) |
 |
Aufgabe |
|
Es soll der Fehler abgeschätzt werden, der an der Stelle x=5 auftritt,
wenn
die Funktion f(x)=e0.5x durch ein Taylorpolynom 2.Grades
approximiert
würde, und man als Entwicklungsstelle xe=e
wählt
(e ist die Eulersche Zahl, also ungefähr 2.718).
Die Formel für die Fehlerabschätzung lautete:
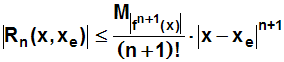
Die Entwicklungsstelle xe ist gleich e (e=Eulersche
Zahl≈2.7182818):
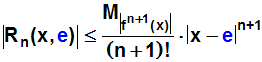
Gesucht ist der Fehler an der Stelle x=5,
also müssen wir für x die Zahl 5 einsetzen:
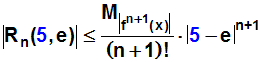
Da das Taylorpolynom vom Grad 2 sein soll,
müssen wir für n die Zahl 2 einsetzen:
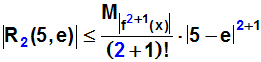
Den Nenner und die Klammer kann man ausrechnen:
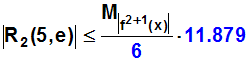
Als nächstes bestimmen wir die 3.Ableitung der Funktion f, also die
3.Ableitung der Funktion f(x)=e0.5x. Durch Anwendung der
Kettenregel bei
jedem Differenzieren erhalten wir f '''(x)=0.125·e0.5x .
Einsetzen in die Formel ergibt:
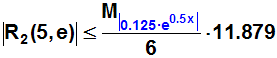
Nun fehlt nur noch der Maximalwert M, den die Ableitungsfunktion
|0.125·e0.5x|
im Intervall [e,5] annehmen kann.
Weil die natürliche Exponentialfunktion streng
monoton steigend ist, wird der größte Wert bei x=5 erreicht, und deshalb
müssen wir x durch 5 ersetzen:
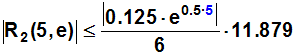
Die rechte Seite der Ungleichung ausrechnen ergibt (gerundet):
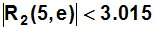
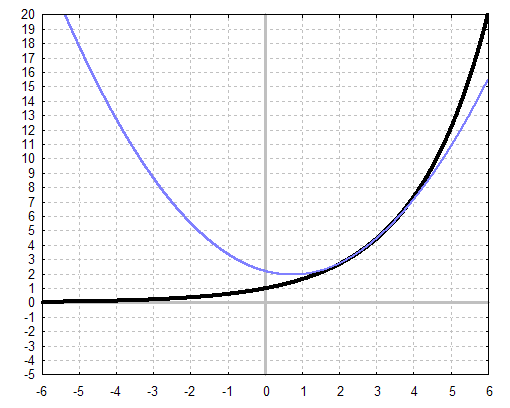
Im Bild unten erkennt man, dass der tatsächliche Fehler an der Stelle
x=5
nur
ungefähr 1 Einheit beträgt. Der tatsächliche Fehler ist also nur 1/3 so
groß,
wie unsere Schätzung R2(5,e)<3.015.
Aber wie schon öfter gesagt,
kann
man mit der Formel den Fehler nur grob abschätzen, aber nicht
berechnen:
 |
| |
|