Manchmal
anwendbarer Trick
zur genaueren
Abschätzung des
Fehlers |
 |
Erklärung |
|
Nehmen wir an, wir wollen die Sinusfunktion sin(x) an der Stelle xe=0
durch ein Taylorpolynom 3.Grades approximieren. Die Taylorformel
für ein Polynom 3.Grades lautet allgemein:
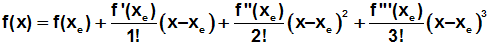
Gegebene Werte einsetzen:
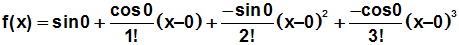
Vereinfachen:
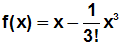
Der Fehler, der bei der Approximation durch ein Polynom 3.Grades
gemacht wird, kann mit der bekannten Formel abgeschätzt werden:
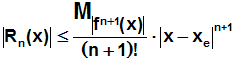
Sie lautet in unserem Fall, also für ein Polynom 3.Grades und xe=0
:
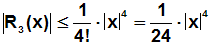
Als Beispiel ergibt sich für die Stelle x=2 eine Fehlerabschätzung von
|R3(2)|<0.666, was weit über dem tatsächlichen Fehler von |R3(2)|=0.242
liegt.
Man kann die Fehlerabschätzung aber in vielen Fällen1
genauer machen,
indem man sich folgendes überlegt:
Im Taylorpolynom der Sinusfunktion für xe=0
(siehe oben) kommen nur
Glieder mit ungeraden Potenzen vor, die geraden Glieder sind gleich
Null.
Daher ist in diesem Fall ein Taylorpolynom 4.Grades identisch
mit einem
Taylorpolynom 3.Grades, denn das Glied mit der
4.Potenz von x entfällt.
Folglich können wir bei der Fehlerabschätzung so tun, als wenn
wir ein
Polynom 4.Grades benutzt hätten, was die Fehlerabschätzung verbessert:
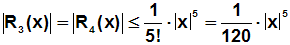
Als Beispiel betrachten wir wieder die Stelle x=2. Es ergibt sich:
Fehler nach dieser Formel: |R3(2)|
< 0.266
Tatsächlicher Fehler zum Vergleich: |R3(2)|=0.242
Die Fehlerabschätzung ist also wesentlich genauer als die
Fehlerabschätzung,
die wir oben gemacht haben, und die |R3(2)|<0.666 betrug.
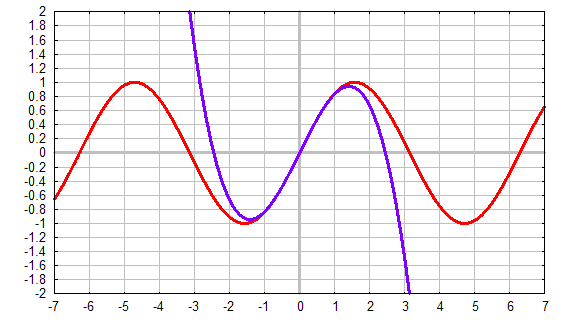 |
| |
1 Man wählt die Entwicklungstelle so, dass eine gerade
oder ungerade
Funktion entsteht. Dann fallen entweder die ungeraden oder geraden
Glieder fort. Ist aber nur bei wenigen Funktionen möglich, nämlich nur
bei Funktionen, die irgendwelche Achsen- oder Punktsymmetrien
besitzen. |
|