|
Hilfssatz 3 |
 |
Hilfssatz 3 |
|
Die Folge xn+1/(n+1)!
konvergiert gegen Null:
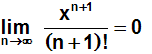
|
|
 |
Beweisüberblick |
|
1. Zunächst beweisen wir die Kongerenz der Reihe:
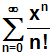
Dazu benutzen wir das
xxxkriterium
2. Die im Schritt 1 genannte Reihe kann aufgrund des
xxxkriteriums nur
konvergieren, wenn die Glieder gegen Null konvergieren, und
somit gilt:
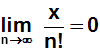
3. Weil die im Schritt 2 genannte Folge gegen Null konvergiert,
konvergiert
nach dem Majorantenkriterium auch die Folge:
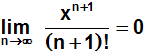
was zu beweisen war. |
| |
|