Vom
Taylorpolynom
zur
Taylorreihe |
 |
Approximation durch
Taylorpolynome
verschiedenen Grades |
|
Im Kurs Taylorpolynome hatten wir gelernt, wie man eine Funktion
in der Nähe eines Punktes xe
approximiert.
Dabei hatten wir gelernt, dass für den Konvergenzbereich des
Taylorpolynoms folgendes gilt:
Der Bereich, in der die Approximation gut ist, kann im allgemeinen
vergrößert
werden, wenn man ein Polynom höheren Grades zur Approximation
benutzt.
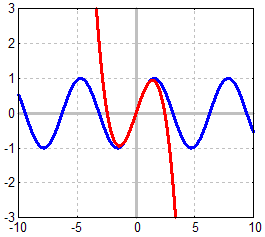
Wir wollen das nochmals veranschaulichen: Im Bild ist die Sinusfunktion
(blau)
durch ein Taylorpolynom 3.Grades (rot) approximiert. Die Approximation
ist
ungefähr zwischen –1 und 1 brauchbar, d.h. Funktion und Polynom
sind fast gleich.
Außerhalb dieses Intervalls wird die Approximation
sehr schnell ungenau:
 |
Die Sinusfunktion (blau) wird durch
ein
Polynom 3. Grades (rot) approximiert:
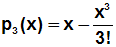 |
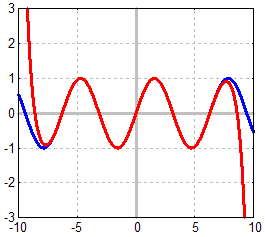
Nun approximieren wir die Sinusfunktion durch ein Taylorpolynom
19.Grades.
Wie man sofort erkennt ist die Approximation in einem viel größeren
Bereich gelungen
(ungefähr von –7 bis 7), weil wir ein Polynom höheren Grades (also mit
vielen Gliedern)
benutzt haben:
 |
Die Sinusfunktion (blau) wird durch
ein Polynom
19. Grades (rot) approximiert:
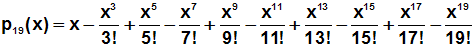 |
Und wählt man ein Taylorpolynom sehr hohen Grades, z.B. ein
Taylorpolynom
43.Grades, dann funktioniert die Approximation über einen noch viel
größeren Bereich.
Im Bild unten wird die Sinusfunktion ca. zwischen –16 und 16 sehr gut
approximiert:
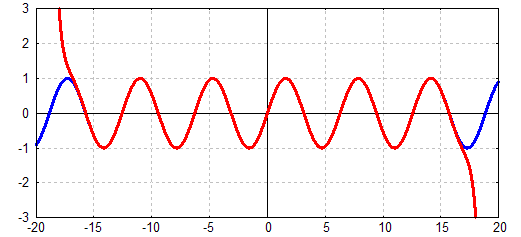 |
Die Sinusfunktion (blau) wird durch
ein
Polynom 43. Grades (rot) approximiert:
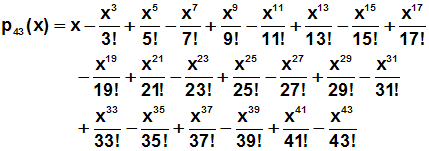 |
|
 |
Approximation durch
Taylorpolynome
unendlichen Grades: |
|
Durch diese Überlegungen taucht automatisch folgende Frage auf:
Wenn ich ein Taylorpolynom mit unendlich vielen Gliedern
nehme,
also ein Taylorpolynom unendlichen Grades, kann ich dann die
Funktion
in ihrem ganzen Definitionsbereich exakt
approximieren?
Die Antwort wird lauten: Ja, im allgemeinen funktioniert das.
Man nennt so ein Taylorpolynom mit unendlich vielen Gliedern
die Taylorreihe der zu approximierenden Funktion.
Die Taylorreihe der Sinusfunktion lautet somit:
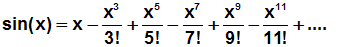
Dabei deuten die Punkte an, dass das Polynom unendlich viele Glieder
hat. |
| |
|