|
Schritt 0:
a0 bestimmen
Nehmen wir an, wir wollen die Taylorreihe der Sinusfunktion bestimmten,
d.h. wir suchen die Potenzreihe, die mit der Sinusfunktion identisch
ist.
Praktisch bedeutet dies, dass wir in der folgenden Gleichung
die
Koeffizienten a0, a1, a2, ...
bestimmen müssen:
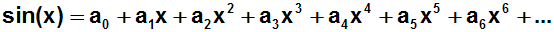
Wir haben gerade gesagt, dass Funktion und Taylorreihe an der
Entwicklungsstelle
gleich sein sollen. Wir setzen also für x die Entwicklungsstelle x=0
ein:
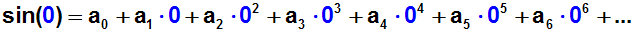
Weil alle Terme nach a0 zu Null werden, erhalten wir den
Koeffizienten a0:
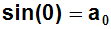
Und weil der Sinus von Null gleich Null ist, ist der Koeffizienten a0
gleich Null:
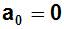
Schritt 1:
a1 bestimmen
Außerdem sollen die Ableitungen von Funktion und Taylorreihe am
Entwicklungspunkt
gleich sein. Wir bilden also die 1.Ableitung der Funktion und der
Taylorreihe (dabei sei
zur Erinnerung gesagt, dass die 1.Ableitung der Sinusfunktion die
Kosinusfunktion ist):
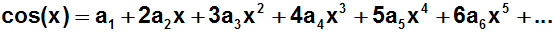
Dann setzen wir für x die Entwicklungsstelle x=0 ein:
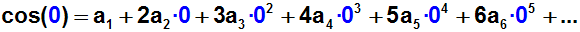
Auf der rechten Seite fallen wie im Schritt 0 wieder alle Terme (außer
dem ersten) weg,
da sie zu Null werden:
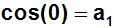
Und weil cos(0)=1 erhalten wir:
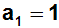
Anmerkung:
Schritt 1 wiederholt sich jetzt immer wieder
Von hier an wiederholt sich Schritt 1 immer wieder, d.h.
wir müssen ableiten und
für x die Entwicklungstelle x=0 einsetzen. Zur Übung machen wir noch ein
paar Schritte:
Schritt 2:
a2 bestimmen
Wir bilden also die Ableitung der Funktion und der Taylorreihe. Dabei
sei zur
Erinnerung gesagt, dass die Ableitung der Kosinusfunktion die Funktion
-sin(x) ist:
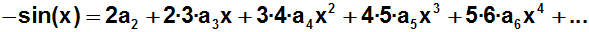
Dann setzen wir wieder für x die Entwicklungsstelle x=0 ein:
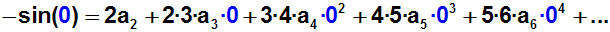
Auf der rechten Seite fallen wieder alle Terme (außer dem ersten) weg,
da sie zu Null werden:
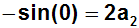
Und weil sin(0)=0 erhalten wir:
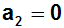
Schritt 3:
a3 bestimmen
Wir bilden also wieder die Ableitung der Funktion und der Taylorreihe.
Dabei sei zur
Erinnerung gesagt, dass die Ableitung der Funktion -sin(x) die Funktion
–cos(x) ist:
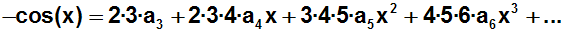
Dann setzen wir dDann setzen wir wieder für x die Entwicklungsstelle x=0
ein:
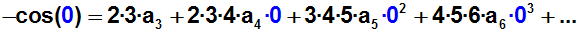
Auf der rechten Seite fallen wieder alle Terme (außer dem ersten) weg,
da sie zu Null werden:
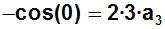
Und weil –cos(0)= –1 erhalten wir:
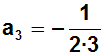
Schritt 4:
a4 bestimmen
Wir bilden also wieder die Ableitung der Funktion und der Taylorreihe.
Dabei sei zur
Erinnerung gesagt, dass die Ableitung der Funktion -cos(x) die Funktion
sin(x) ist:
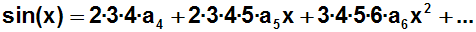
Dann setzen wir wieder für x die Entwicklungsstelle x=0 ein:

Auf der rechten Seite fallen wieder alle Terme (außer dem ersten) weg,
da sie zu Null werden:
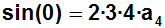
Und weil sin(0)= 0 erhalten wir:
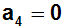
Schritt 5:
a5 bestimmen
Wir bilden also wieder die Ableitung der Funktion und der Taylorreihe.
Dabei sei zur
Erinnerung gesagt, dass die Ableitung der Funktion sin(x) die Funktion
cos(x) ist:
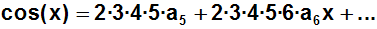
Dann setzen wir wieder für x die Entwicklungsstelle x=0 ein:
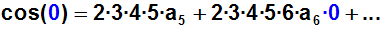
Auf der rechten Seite fallen wieder alle Terme (außer dem ersten) weg,
da sie zu Null werden:
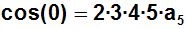
Und weil cos(0)= 1 erhalten wir:
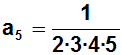
Zusammenfassung
von Schritt 1-5:
Wir haben jetzt die ersten sechs Koeffizienten berechnet.
Sie lauten:
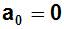
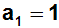
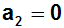
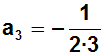
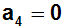
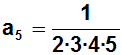
Berechnete
Koeffizienten in den Ansatz einsetzen:
Der Ansatz, den wir machten, lautete:
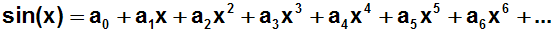
Am Ende müssen wir alle Koeffizienten (soweit wir sie berechnet haben)
in die Potenzreihe einsetzen, also die Koeffizienten a0, a1,
a2, a3, a4, a5:
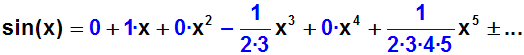
Vereinfachen:
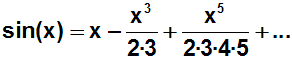
Um die Fakultät-Schreibweise einführen zu können, dividieren wir alle
Terme durch 1:
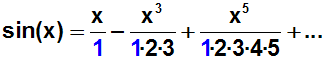
Dadurch können wir die abkürzende Fakultätschreibweise anwenden:
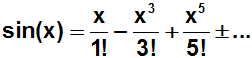
Bildungsgesetz erkennen:
Jetzt erkennen wir das Bildungsgesetz: Im Zähler stehen nacheinander
alle
ungeraden Potenzen von x, im Nenner eine gleichnamige Fakultät und
das Vorzeichen der Terme wechselt zwischen PLUS und MINUS.
Hat man das Bildungsgesetz erkannt, und können beliebig viele Glieder
der Reihe angeben, z.B die ersten zehn Glieder:
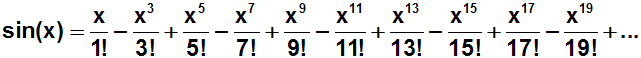
|