Taylorreihen
für die
Entwicklungstelle
x=0 |
 |
Formel für die Taylorreihe
(Entwicklungsstelle x=0) |
|
Im Kurs Taylorpolynome haben wir u.a. eine Formel entwickelt, mit der
man ein Taylorpolynom an der Entwicklungsstelle
xe=0 herleiten kann:
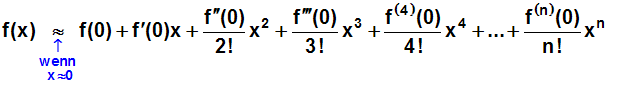
In der Schreibweise mit dem Summenzeichen lautete die Formel:
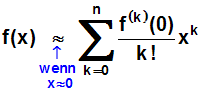
Nun wollen wir die Funktion nicht nur lokal approximieren, wie im Kurs
Taylorpolynome, sondern wir wollen die Funktion global ersetzen:
Das bedeutet, die Funktion soll nicht nur
approximiert werden,
sondern das Polynom soll der Funktion exakt entsprechen.
Zweitens soll dies im ganzen Definitionsbereich der
Funktion der Fall sein,
und nicht nur in der Nähe der Entwicklungsstelle.
Um dies zu erreichen, muß das Taylorpolynom unendlich viele
Glieder
haben (Beweis im Kapitel 3). Man spricht dann nicht von einem
Taylorpolynom,
sondern von einer Taylorreihe. Die Taylorreihe hat nicht nur n Glieder,
wie das Taylorpolynom, sondern unendlich viele Glieder.
In der Formel für die Taylorreihe müssen wir also das
Ungefähr-Zeichen (≈)
durch ein Gleichheitszeichen (=) ersetzen und die Anzahl der
Glieder
unendlich werden lassen. Die Formel für eine
Taylorreihe an der
Entwicklungsstelle x=0 lautet daher:
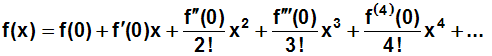
Auch in der Summenzeichen-Schreibweise müssen wir n durch
∞ ersetzen,
und das Ungefähr-Zeichen (≈) durch ein Gleichheitszeichen (=):
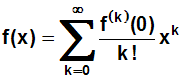
Mit den letzten beiden Formeln (vorzugsweise mit der vorletzten) können
wir
nun eine Funktion global durch ihre Taylorreihe ersetzen.
Man sagt: Wir entwickeln die
Funktion an der Stelle x=0.
Wenn wir, wie auf dieser Seite, eine Funktion an der Stelle x=0
entwickeln,
dann nennt man die Taylorreihe auch oft
McLaurin Reihe.
|
 |
Beispiel |
|
Wie heißt die Taylorreihe der Kosinusfunktion cos(x), wenn sie an der
Stelle
x=0 entwickelt wird? Die Formel der Taylorreihe haben wir gerade
kennengelernt:
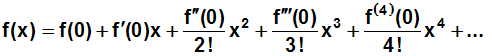
Weil die Taylorreihe der Kosinusfunktion gesucht ist, ersetzen wir f(x)
durch cos(x):
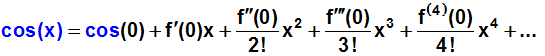
Weil auch die Ableitungen f ', f '' , f ''', ... in der Formel benötigt
werden, müssen wir
die Ableitungen der Kosinusfunktion in der Formelsammlung nachschlagen,
und sie in der Formel ersetzen. Die Ableitungen lauten:
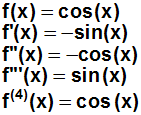
Einsetzen in die Formel ergibt:
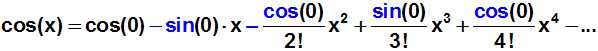
Mit dem Taschenrechner sin(0)=0 und cos(0)=1 berechnen, und in die
Formel einsetzen:
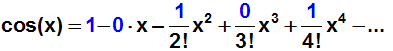
Vereinfachen: Manche Glieder fallen weg, weil der Faktor Null vorkommt.
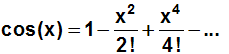
Dies ist die Taylorreihe von cos(x), entwickelt an der Stellle x=0,
denn wir können das Bildungsgesetz dieser Reihe nun gut erkennen:
Es kommen nur gerade Potenzen vor, die jeweils durch eine Fakultät
dividiert werden, deren Argument gleich dem Exponenten ist.
Außerdem wechselt das Vorzeichen nach jedem Glied.
Auch das erste Glied folgt dabei diesen Regeln, denn es gilt:
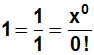
Man kann zum besseren Erkennen dieser Regel auch mehr Glieder
der Reihe angeben, z.B. die ersten sieben Glieder:
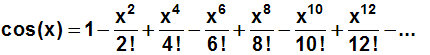 |
| |
|