|
Entwicklung an beliebiger Stelle |
 |
Formel für die Taylorreihe an
der Entwicklungstelle x=xe |
|
Die Formel für ein Taylorpolynom, dass an der Stelle xe
entwickelt werden soll,
haben wir im Kurs Taylorpolynome kennengelernt:
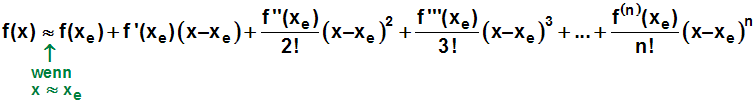
bzw. in der Schreibweise mit dem Summenzeichen:
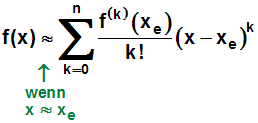
Die Formel für die Taylorreihe lautet ähnlich, bis auf zwei
Unterschiede: Die Taylorreihe
hat unendlich viele Glieder
anstatt nur n Glieder. Außerdem muß das "Ungefährzeichen" durch
ein Gleichheitszeichen ersetzt werden:
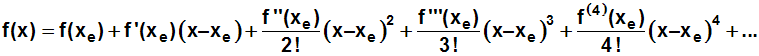
bzw. in der Schreibweise mit dem Summenzeichen:
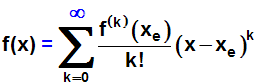
|
 |
Beispiel: Taylorreihe von
cos(x) für xe=π |
|
Wir suchen die Taylorreihe für cos(x) an der Entwicklungsstelle xe=π.
Die Taylorreihe für eine beliebige Entwicklungsstelle haben wir soeben
kennengelernt. Sie lautete:
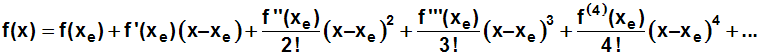
Wir ersetzen die Funktion f(x) bzw. ihre Ableitungen durch cos(x) bzw.
ihre Ableitungen:
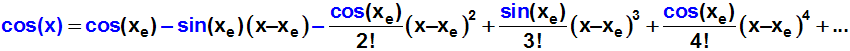
Die Entwicklungsstelle xe ist gleich
π, also ersetzen wir xe
überall durch π:
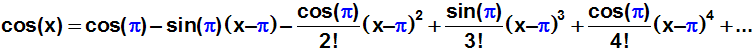
Die Funktionswerte sin(π) und cos(π) können
mit dem Taschenrechner berechnet werden, sie sind gleich Null bzw. –1:
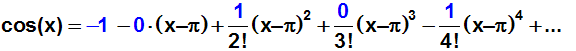
Vereinfachen: Die Terme in denen der Faktor Null vorkommt fallen weg:
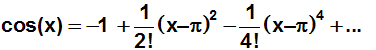
|
| |
|