Hinreichendes
Kriterium für die
Existenz der
Taylorreihe |
 |
Satz |
|
Ein hinreichendes Kriterium für die Existenz der Taylorreihe
ist
die Existenz aller Ableitungen der Funktion. |
Beachte, dass die Existenz der Taylorreihe einer Funktion noch
nicht beweist, dass die Funktion und ihre Taylorreihe übereinstimmen.
Diese Frage wird nämlich erst im nächsten Kapitel behandelt.
|
 |
Erklärung des Satzes |
|
Betrachten wir nochmal die Formel für eine Taylorreihe:
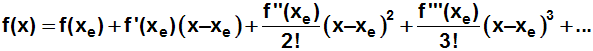
Wie man sieht, kommen in der Formel alle Ableitungen der Funktion vor.
Damit eine Funktion eine Taylorreihe besitzt, ist es also notwendig,
dass alle Ableitungen der Funktion existieren.
Weil die Formel ansonsten keine weiteren Forderungen an die Funktion
f(x) stellt,
ist diese Bedingung auch hinreichend für die Existenz der
Taylorreihe.
|
| |
|