Notwendige
Bedingung für
die Konvergenz
der Taylorreihe
gegen die Funktion:
Die Taylorreihe
muß
konvergieren,
d.h. sie darf
nicht divergieren |
 |
Worum geht es |
|
Eine notwendige Bedingung dafür, dass eine Funktion f durch eine Reihe
ausgedrückt
werden kann, ist die Konvergenz der Reihe im
Definitionsbereich
der Funktion.
|
 |
Beispiel |
|
Die Taylorreihe der Funktion f(x)=1/(1–x) hat den Konvergenzbereich
(–1,1), den man
mit den üblichen Test berechnen kann. Außerhalb dieses Bereichs divergiert die
Taylorreihe
für n gegen Unendlich, d.h. sie schießt wie eine Rakete ins Unendliche
bzw fällt ins Unendliche.
Daher kann die Tayorreihe nur innerhalb ihres Konvergenzbereichs die
Funktion f(x) darstellen,
denn wenn die Funktion ins Unendliche geht, kann sie nicht gleichzeitig
mit einer endlichen Funktion übereinstimmen.
Daher wird außerhalb des Konvergenzbereichs (–1,1)
die Approximation sogar schlechter,
wenn die Anzahl der Glieder größer wird, denn je mehr Glieder die
Taylorreihe hat, desto
eher divergiert sich nach oben bzw. unten ins Unendliche, sobald man den
Konvergenzbereich verläßt.
Die folgende Animation zeigt den Sachverhalt (Die Animation erhöht jede
Sekunde die Anzahl der Glieder):
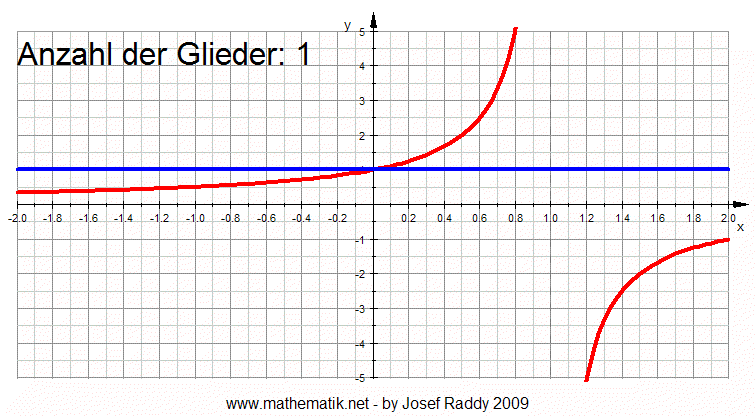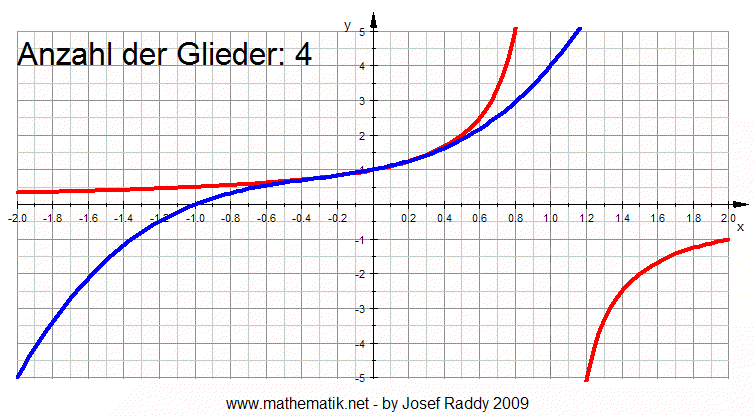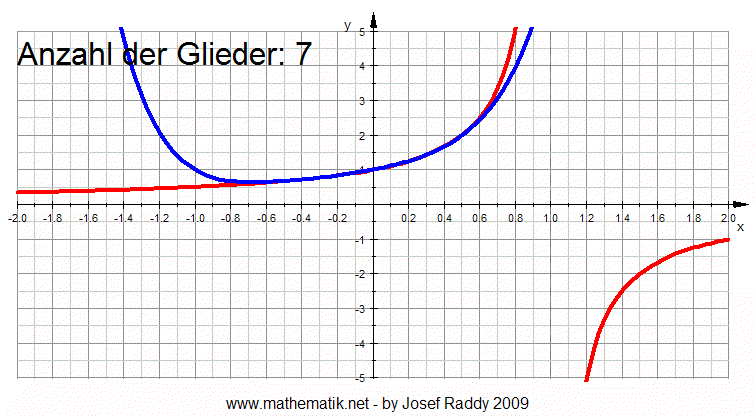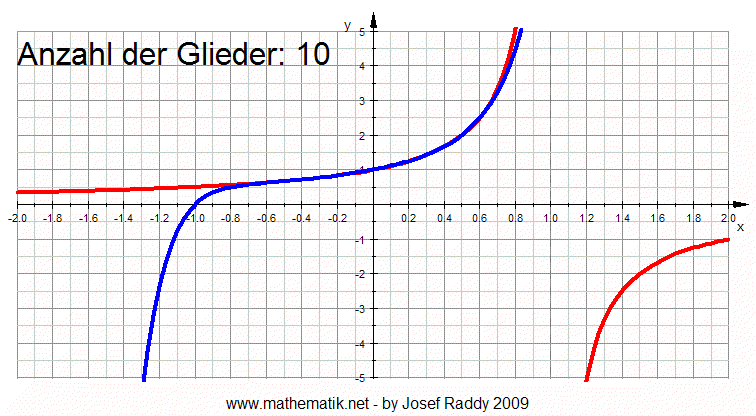
|
 |
Hinweis: Die Bedingung ist
notwendig aber nicht hinreichend |
|
Man beachte: Die Konvergenz der Taylorreihe in dem Bereich, in dem sie
die Funktion darstellen soll,
ist eine notwendige aber keine hinreichende Bedingung für
die Konvergenz der Taylorreihe gegen die Funktion:
Es gibt nämlich (wenn auch selten) Funktionen,
deren
Taylorreihe zwar konvergiert, aber nicht gegen die Funktion.
Das klassische Beispiel stammt von Cauchy, und ist in jedem Lehrbuch zu
finden:
Entwickelt man zur Funktion f (roter Graph) die zugehörige
Taylorreihe (blau) an der
Entwicklungsstelle x=0
dann konvergiert die Taylorreihe, aber nicht gegen die Funktion,
sondern
gegen die Null (Nullfunktion).
Genauer gesagt: Die Taylorreihe (blau)
der Funktion f (rot) konvergiert nur an der Stelle x=0
gegen die Funktion f:
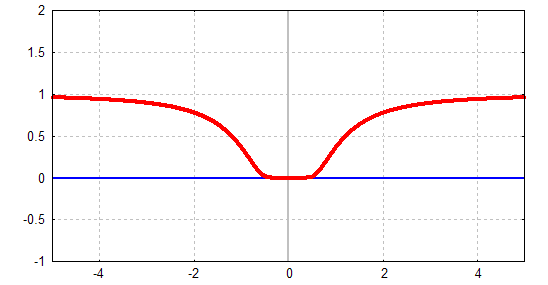
Der Graph der Funktion (rot) verläuft nämlich so flach um Ursprung, dass
alle Ableitungen
an der Stelle x=0 zu Null werden (der exakte Beweis wird hier
übergangen).
Daher lautet die Taylor-Serie mit der Entwicklungsstelle x=0:
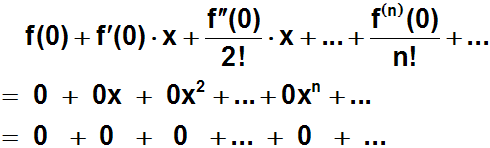
Und daher ist die Taylorreihe von f die Nullfunktion (wenn man sie an
der Stelle x=0 entwickelt). |
| |
|